Запишем формулу мощности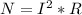 
, где I - действующая сила тока (А), R - сопротивление проводника (спирали) (Ом). Сопротивление расписываем как 
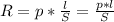, где l - длина проводника (спирали), S - поперечное сечение проводника (м²), р - удельное сопротивление проводника (Ом*м). Подставив данную формулу в формулу мощности получим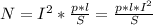 
Первоначальная мощность утюга равна 300 Вт, затем спираль сократили на ¼. Отсюда получаем зависимость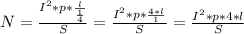 
. Как получили зависимоть прямая т.е. можно сотавить соотношение
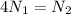- конечная мощность утюга (после укорочения спирали) в 4 раза боьше первоначальной мощности. Тогда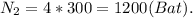 
Первая задача
Собственная длина космического корабля 15 м. Определить его длину для наблюдателя, находящегося на корабле, и для наблюдателя, относительно которого корабль движется со скоростью 1,8∙108 м/с.
Вторая задача
Движение априори предполагает скорость. Опять же, скорость отрицательной быть не может, поэтому есть либо состояние покоя, либо движение (оно тождественно скорости). Есть правда гипотезы на уровне фантастики, что в черных дырах пространство и время текут в обратном от Земли порядке, так что там такое возможно возможно))) сорри за тавтологию!
Третья задача
Энергия покоя mc^2.
В классике кин. энергия mv^2/2, приравняем и получим v = корень(2) * c (выше скорости света!).
В релятивизме квадрат полной энергии E^2 = (mc^2)^2 + (pc)^2 = по условию задачи = (2mc^2)^2
импульс p = Ev / c^2 = 2mv
подставляем опять в уравнение для энергии,
(mc^2)^2 + (2mvc)^2 = (2mc^2)^2
в общем, решаем простенькое уравнение и получаем v = корень(3)/2 * c = примерно 0,866 c
Четвертая задача
M = m / √(1 - 0.64c²/с²) = m / 0.36
Объяснение:
Дано:
m₁ = 20 т = 20 000 кг
v₁ = 3 м/с
v₂ = 2 м/с
u = 2,4 м/с
m₂ - ?
1)
Импульс системы до сцепки:
p₀ = m₁·v₁ + m₂·v₂
2)
Импульс системы после сцепки:
p₁ = (m₁+m₂)·u
3)
По закону сохранения импульса:
p₀ = p₁
m₁·v₁ + m₂·v₂ = (m₁+m₂)·u
m₁·v₁ + m₂·v₂ = m₁·u +m₂·u
m₂·u - m₂·v₂ = m₁·v₁ - m₁·u
m₂·(u - v₂)= m₁·(v₁ - u)
m₂ = m₁·(v₁ - u) / (u - v₂) = 20 000·(3-2,4) / (2,4-2) = 40 000 кг или 40 т