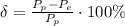
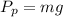 (1)
(1)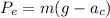 )
)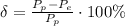 (3)
(3)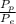 . Т.е спросить во сколько раз скажем полярный вес больше экваториального.
. Т.е спросить во сколько раз скажем полярный вес больше экваториального.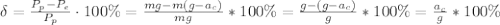 (4
(4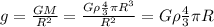 (5)
(5)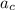 :
: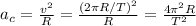 (6)
(6)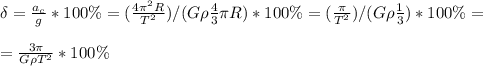
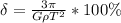 (6)
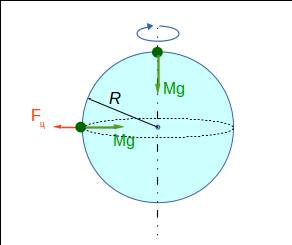
(6)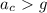 ? В этом случае любое тело улетит с экватора. Тогда и пользоваться формулой (6) некорректно.
? В этом случае любое тело улетит с экватора. Тогда и пользоваться формулой (6) некорректно.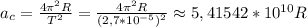
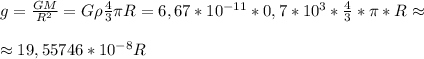

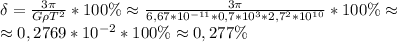
 есть функция от глубины z.
есть функция от глубины z.
 (3)
(3) (4)
(4)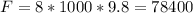 Н
Н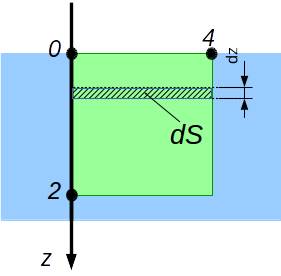
ответ:192см
Объяснение:3+90×2,1