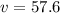 км/ч
км/ч  м/с
м/с 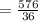 м/с
м/с 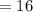 м/с.
м/с.


 м .
м .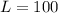 м .
м .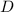 в [м] и [мм].
в [м] и [мм]. и это означает, что каждые
и это означает, что каждые 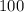 секунд, в положении Н оказывается Начало очередного состава. Уже припаркованный состав простоял на станции
секунд, в положении Н оказывается Начало очередного состава. Уже припаркованный состав простоял на станции 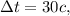 а это означает, что следующему за ним составу осталось проехать из положения С (начало скоростного состава) до точки Н (начало припаркованного состава) в течение
а это означает, что следующему за ним составу осталось проехать из положения С (начало скоростного состава) до точки Н (начало припаркованного состава) в течение 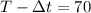 секунд.
секунд.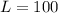 м.
м.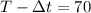 секунд, оставшихся идущему следом составу, первые
секунд, оставшихся идущему следом составу, первые  секунд он будет идти с постоянной скоростью
секунд он будет идти с постоянной скоростью 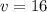 м/с из положения С в положение О, а последующие
м/с из положения С в положение О, а последующие  секунд он будет останавливаться из положения О до положения Н.
секунд он будет останавливаться из положения О до положения Н. м . Теперь найдём СО, т.е. длину
м . Теперь найдём СО, т.е. длину 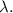 Мы знаем, что по отрезку СО состав двигается равномерно со скоростью
Мы знаем, что по отрезку СО состав двигается равномерно со скоростью  в течение времени
в течение времени  секунд, значит отрезок СО, т.е.
секунд, значит отрезок СО, т.е. 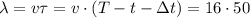 м
м  м .
м . м
м 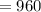 м.
м.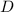 – это длина СК, равная разности СН и КН, т.е. СН и
– это длина СК, равная разности СН и КН, т.е. СН и 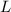 .
.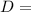 СК
СК  CH
CH 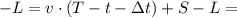
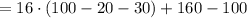 м
м  м.
м.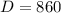 м
м  мм .
мм .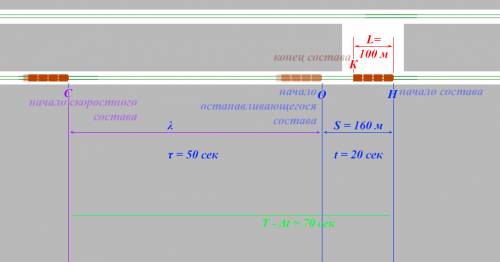
m=5 кг g=10 м/c^2 a=3 м/с^2
По 2 Закону Ньютона:
mg(ветор)+T(вектор)=ma(вектор)
В проекции на ось Х:
Т-mg=ma (тут уже векторы не нужны, т.к мы уже спроецировали)
Далее выражаем отсюда силу натяжения нити - T, получаем:
T=ma+mg=m(a+g)
Мы получили ответ в общем виде, теперь нам надо подставить туда наши значения:
Т=5 кг * ( 3 + 10) м/с^2 = 65 Н
Отв. 65 Н