1. Водитель автомобиля начал торможение, когда находился на расстоянии 200 м от заправочной станции и двигался к ней со скоростью 20 м/с. Какой должна быть сила торможения, чтобы автомобиль массой 1 т остановился около станции?
Дано:
м
м/с
т кг
Найти:
Решение. Направим горизонтальную ось в сторону торможения автомобиля. Перейдем от проекций к модулям:
Тогда откуда
Применим второй закон Ньютона:
Определим значение искомой величины:
ответ: 1 кН
2. Сани движутся по горизонтальной дороге с начальной скоростью 5 м/с, коэффициент трения при этом равен 0,1. Найдите путь, который сани за 3 с.
Дано:
м/с
м/с²
Найти:
Решение. Направим горизонтальную ось в сторону движения саней. Перейдем от проекций к модулям:
Тогда откуда
Найдем
Применим второй закон Ньютона:
Сила трения:
Поскольку , то
Таким образом,
Определим значение искомой величины:
м
ответ: 19,5 м.
3. Автобус массой 10 т, двигаясь с места, развил на пути 50 м скорость 10 м/с. Найдите коэффициент трения, если сила тяги равна 14 кН.
Дано:
т кг
м
м/с
кН
м/с²
Найти:
Решение. Направим горизонтальную ось в сторону движения автобуса. Перейдем от проекций к модулям:
В общем и целом, модель материальной точки применима тогда, когда мы можем пренебречь размерами и формой тела. Исходя из этого, считать Луну материальной точкой
При расчете расстояния от Земли до Луны: Можно, так как расстояние от Земли до Луны существенно больше размеров Луны.
При измерении диаметра Луны: Нельзя, так как размеры Луны нас, собственно, и интересуют.
При расчете движения спутника вокруг Луны: Можно, при условии, что спутник находится на достаточно большой высоте, чтобы размеры Луны можно было бы считать пренебрежительно малыми.
При посадке космического корабля на ее поверхность: Нельзя, так как материальная точка не имеет поверхности.
При определении скорости ее движения вокруг Земли: Можно по той же причине, что и в п. 1.
1. Водитель автомобиля начал торможение, когда находился на расстоянии 200 м от заправочной станции и двигался к ней со скоростью 20 м/с. Какой должна быть сила торможения, чтобы автомобиль массой 1 т остановился около станции?
Дано:
Найти: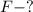
Решение. Направим горизонтальную ось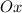 в сторону торможения автомобиля. Перейдем от проекций к модулям:
в сторону торможения автомобиля. Перейдем от проекций к модулям:
Тогда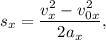 откуда
откуда 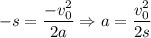
Применим второй закон Ньютона: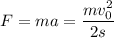
Определим значение искомой величины:
ответ: 1 кН
2. Сани движутся по горизонтальной дороге с начальной скоростью 5 м/с, коэффициент трения при этом равен 0,1. Найдите путь, который сани за 3 с.
Дано:
Найти: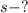
Решение. Направим горизонтальную ось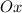 в сторону движения саней. Перейдем от проекций к модулям:
в сторону движения саней. Перейдем от проекций к модулям:
Тогда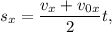 откуда
откуда 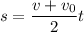
Найдем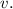
Применим второй закон Ньютона: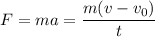
Сила трения: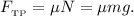
Поскольку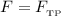 , то
, то
Таким образом,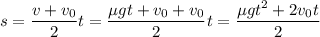
Определим значение искомой величины:
ответ: 19,5 м.
3. Автобус массой 10 т, двигаясь с места, развил на пути 50 м скорость 10 м/с. Найдите коэффициент трения, если сила тяги равна 14 кН.
Дано:
Найти: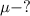
Решение. Направим горизонтальную ось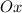 в сторону движения автобуса. Перейдем от проекций к модулям:
в сторону движения автобуса. Перейдем от проекций к модулям:
Тогда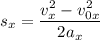 , откуда
, откуда 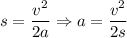
Применим второй закон Ньютона: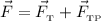
Перейдем от векторов к модулям:
Определим значение искомой величины:
ответ: 0,04.