За законом Ома, напруги U1 і U2 на провідниках рівні
U1 = IR1, U2 = IR2.
Загальна напруга U на обох провідниках дорівнює сумі напруги U1 і U2:
U = U1 + U2 = I(R1 + R2) = IR,
де R – електричний опір всього кола. Звідси слідує:
R=R1+R2
2.
Послідовне і паралельне з'єднання провідників
Провідники в електричному колі можуть з'єднуватися послідовно і паралельно.
Послідовне з'єднання
При послідовному з'єднанні провідників (мал. 1.) сила струму у всіх провідниках однакова:
I1 = I2 = I.
Малюнок 1.
Послідовне з'єднання провідників
За законом Ома, напруги U1 і U2 на провідниках рівні
U1 = IR1, U2 = IR2.
Загальна напруга U на обох провідниках дорівнює сумі напруги U1 і U2:
U = U1 + U2 = I(R1 + R2) = IR,
де R – електричний опір всього кола. Звідси слідує:
R = R1 + R2.
При послідовному з'єднанні повний опір кола дорівнює сумі опорів окремих провідників.
Цей результат справедливий для будь-якого числа послідовно з'єднаних провідників.
Паралельне з'єднання
При паралельному з'єднанні (мал. 2) напруга U1 і U2 на обох провідниках однакові:
U1 = U2 = U.
Сума струмів I1 + I2 , що протікають по обох провідниках, дорівнює струму в нерозгалуженому колі:
I = I1 + I2.
Цей результат виходить з того, що в точках розгалуження струмів (вузли A і B) у колі постійного струму не можуть накопичуватися заряди. Наприклад, до вузла A за час t приходить заряд I*t а виходить з вузла за той же час заряд I1*t + I2*t. Отже
I = I1 + I2.
Малюнок 2.
Паралельне з'єднання провідників
Записуючи на підставі закона Ома
де R – електричний опір всього кола, отримаємо
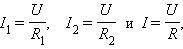
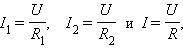
не только числа, но и символьные обозначения всех ( р е ш е н и й ).
Из чисел и букв можно составлять равенства – ( ф о р м у л ы ).
Например, по формуле l = 2pR можно узнать ( д л и н у ) окружности,
а по формуле S = pR2 можно ( в ы ч и с л и т ь ) площадь круга.
То есть, формулы – это ( п р а в и л а ) вычисления величин,
записанные с общепринятых символьных ( о б о з н а ч е н и й ). Все формулы можно преобразовывать по следующим правилам ( а л г е б р ы ).
Чтобы найти неизвестное слагаемое, нужно из ( с у м м ы ) вычесть
известное ( с л а г а е м о е ).
...Чтобы найти неизвестный множитель,
нужно ( п р о и з в е д е н и е ) разделить на известный множитель
...Чтобы найти неизвестное уменьшаемое, нужно ( с л о ж и т ь )
разность и ( в ы ч и т а е м о е )
...Чтобы найти вычитаемое,
из уменьшаемого вычитают ( р а з н о с т ь ).
...Чтобы найти ( д е л и м о е ), нужно перемножить частное и делитель,
...Чтобы найти делитель, нужно делимое ( р а з д е л и т ь ) на частное.