В том месте, где сосуды сообщаются, давления в первом и втором на одинаковой высоте равны. Скорее всего, в этом месте у вас вода на рисунке - проверьте. И на поверхностях сосудов давления тоже равны (атмосферному, то есть нулевому, если атмосферное не учитывать).
Ну а дальше считайте давление по формуле плотность*g*высота столбика И, если одна жидкость налита поверх другой, то складывайте давления от столбиков жидкости, получите суммарное...
Дальше - алгебра. Ну и плотности жидкостей нужно в учебнике посмотреть - там они округлены так, чтобы в седьмом классе вас не напрягать арифметикой слишком сильно. В справочнике не стоит смотреть
1. 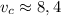 км/ч
км/ч
2. 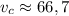 км/ч
км/ч
Объяснение:
1.
Дано:
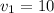 км/ч
км/ч
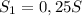
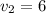 км/ч
км/ч
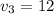 км/ч
км/ч
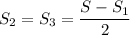
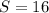 км
км
Найти:
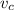 - ?
- ?
----------------------------------
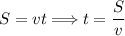
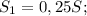
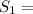 0,25 * 16 км = 4 км;
0,25 * 16 км = 4 км;
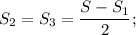
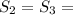 (16 км - 4 км) / 2 = 12 км / 2 = 6 км;
(16 км - 4 км) / 2 = 12 км / 2 = 6 км;
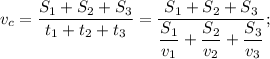
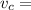 (4 км + 6 км + 6 км) / (4 км / 10 км/ч + 6 км / 6 км/ч + 6 км / 12 км/ч) =
(4 км + 6 км + 6 км) / (4 км / 10 км/ч + 6 км / 6 км/ч + 6 км / 12 км/ч) =
16 км / (0,4 ч + 1 ч + 0,5 ч) = 16 км / 1,9 ч ≈ 8,4 км/ч;
ответ: 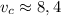 км/ч.
км/ч.
2.
Дано:
 км
км
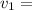 100 км/ч
100 км/ч
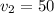 км/ч
км/ч
Найти:
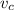 - ?
- ?
----------------------------------
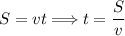
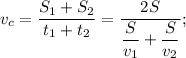
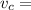 (2 * 14 км) / ( (14 км / 100 км/ч) + (14 км / 50 км/ч)) =
(2 * 14 км) / ( (14 км / 100 км/ч) + (14 км / 50 км/ч)) =
= 28 км / (0,14 ч + 0,28 ч) = 28 км / 0,42 ч ≈ 66,7 км/ч;
ответ: 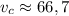 км/ч.
км/ч.
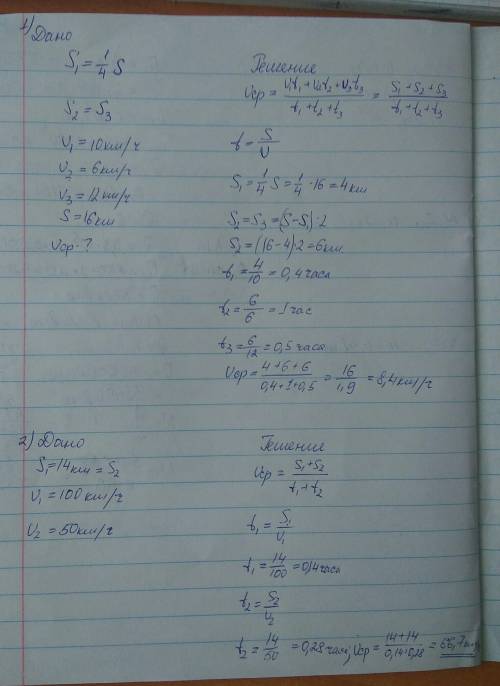
ответ: решение во вложении