Question

Главное фокусное расстояние собирающей линзы равно F. На каком расстоянии нужно поместить предмет, чтобы увеличение было больше 2, но меньше 3?​

Answer 1

1,33F<d<1.5F

Объяснение:

Воспользуемся формулой тонкой линзы

$\frac{1}{d}+\frac{1}{f} =\frac{1}{F}$

Теперь вспомним что линейное увеличение линзы равно отношению высоты изображения к высоте предмета или же отношению расстояния от линзы до изображения к расстоянию от предмета до линзы (следует из подобных треугольников, образованных лучом, идущим вдоль побочной оптической оси, главной оптической осью линзы, предметом и изображением)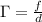 $\Gamma =\frac{f}{d}$

Преобразуем формулу тонкой линзы, выделив из нее увеличение

$1+\frac{1}{\Gamma } =\frac{d}{F}$

$\Gamma =\frac{F}{d-F}$

Решим неравенство (d-F>0 иначе изображение было бы мнимым)

$2$

$\left \{ {{F2d-2F} \atop {F$

$\left \{ {{d1.33F}} \right.$

Или d лежит в интервале (1,33F,1.5F).