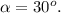 Стало быть, сила, действующая на клин – будет придавать вертикальный импульс и скорость в
Стало быть, сила, действующая на клин – будет придавать вертикальный импульс и скорость в 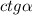 раз больший, чем горизонтальный импульс и скорость.
раз больший, чем горизонтальный импульс и скорость.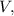 тогда его вертикальная скорость
тогда его вертикальная скорость 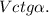
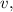 а вертикальную, как
а вертикальную, как 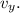
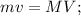
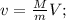
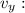
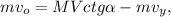
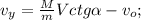
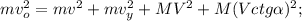
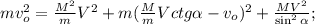
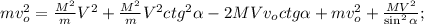
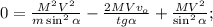
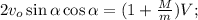
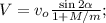
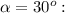
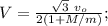
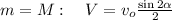 ;
;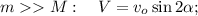
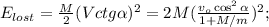
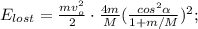
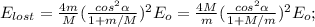
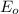 – начальная кинетическая энергия.
– начальная кинетическая энергия.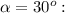
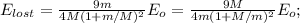
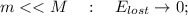
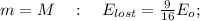
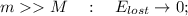





При торможении до конца остановки
выделилось Q(2)=624Дж теплоты.
Объяснение:
h=16м
m=5кг
g=9,8н/кг
Q(1)=160Дж
V(конеч.) =0
Q(2)=?
Санки находятся на вершине горы.
Если за нулевой уровень считать
ее подножие, то потенциальная
энергия санок на вершине:
Е(пот.)=mgh
E(пот.)=5кг×9,8кг×16м=784Дж
В этот момент санки неподвижны,
поэтому не имеют кинетической
энергии. Во время спуска по склону
часть потенциальной энергии пере
ходит в кинетическую (санки разго
няются), а другая ее часть уходит на
нагревание льда (преодоление си
лы трения между полозьями и повер
хностью льда).
Е(пот.)=Е(кин.)+Q(1)
После завершения спуска кинети
ческая энергия санок максимальна,
а потенциальная энергия равна 0
(достигнут нулевой уровень). После
спуска движение происходит по го
ризонтальной поверхности до пол
ной остановки. Вся кинетическая
энергия санок затрачивается (в ре
зультате действия сил трения) на
нагревание пушистого снега:
Q(2)=E(кин.)=Е(пот.)-Q(1)
Q(2)=784Дж-160Дж=624Дж
ответ: 624Дж.