На шарик действуют две силы - сила тяжести, направленная вниз и сила сопротивления воздуха, направленная вверх. Второй закон Ньютона в проекции на ось y запишется в виде
Или, в дифференциальной форме
Однако ускорение , значит
Поместим правую часть под знак дифференциала
Перенесем все в левую часть
Значит выражение в скобках является постоянной величиной
Константу интегрирования найдем из начальных условий
Значит
Рассмотрим теперь конечное состояние тела (), подставив все это в полученное уравнение найдем коэффициент сопротивления (знак минус возник из-за не совсем правильного выбора направления оси у, на самом деле ось надо было направить вниз, поэтому просто возьмем значение по модулю, решение было проверено через точное решение дифференциального уравнения но эти выкладки здесь будут излишними ввиду их громоздкости и сложности)
Задачу можно решить через кинематику и динамику, а можно через закон сохранения энергии и работу, я распишу второй вариант. В таком случае получаем, что начальная энергия тела: E1=mgH. Затем на тело действовала сила сопротивления Fc, а так же потенциальная энергия трансформировалась в кинетическую, т.е. E2=mv^2/2 Работы против силы сопротивления численно равна модулю силы на перемещение(аналог силы трения), т.е. Ac=Fс*H
Таким образом: E1=E2+Ac. Подставляем выражения, полученные выше, и получаем: FcH=mv^2/2-mgH, откуда Fc=(m/h)*(gh-v^2/2). Подставляем все исходные данные получаем ответ 1.4 при g=10 (или 1.3 при g=9.8).
0,02 Н*с/м
Объяснение:
На шарик действуют две силы - сила тяжести, направленная вниз и сила сопротивления воздуха, направленная вверх. Второй закон Ньютона в проекции на ось y запишется в виде
Или, в дифференциальной форме
Однако ускорение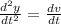 , значит
, значит
Поместим правую часть под знак дифференциала
Перенесем все в левую часть
Значит выражение в скобках является постоянной величиной
Константу интегрирования найдем из начальных условий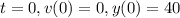
Значит
Рассмотрим теперь конечное состояние тела (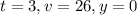 ), подставив все это в полученное уравнение найдем коэффициент сопротивления (знак минус возник из-за не совсем правильного выбора направления оси у, на самом деле ось надо было направить вниз, поэтому просто возьмем значение по модулю, решение было проверено через точное решение дифференциального уравнения но эти выкладки здесь будут излишними ввиду их громоздкости и сложности)
), подставив все это в полученное уравнение найдем коэффициент сопротивления (знак минус возник из-за не совсем правильного выбора направления оси у, на самом деле ось надо было направить вниз, поэтому просто возьмем значение по модулю, решение было проверено через точное решение дифференциального уравнения но эти выкладки здесь будут излишними ввиду их громоздкости и сложности)