1) Лёд очень слабее сжимается при охлаждении, чем метал. Образовав корку вокруг провода, он не позволяет сжиматся роводу далее. Провод натягивается всё сельней извнутри, но лёд хорошо выдерживает сжимающие нагрузки. Ничем не скомпенсированное напряжение натяжения в проводе, в конце концов "рвёт" его.
Можно сказать так: Лёд образует оболочку, которая не позволяет проводу свободно гнутся
(при ветре и.т.п.) и появляются силы действующие на излом провода.
2) Равнодействующая двух приложенных сил может иметь различные значения. В первую очередь имеет значение угла между прилагаемыми силами. А вообще используется правило паралелограмма т.е. две приложенные силы есть векторы имеющие угол между собой, изходя из этого, по двум векторам дотраиваю паралелограмм.
Так же можно использовать правило треугольника.
3) ила упругости это и есть жёсткость т.е. использование формулы закона Гука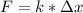 
, где F - сила упругости (Н), k - жёсткость пружины (Н/м), Δх - относильное удлинение (м).
4) Могу дать формулу ⇒
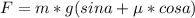
5) 
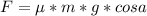Сила трения движущегося тела по наклоной плоскрости.
6) За счёт большего диаметра, получается больший рычаг. Следовательно чем больше руль управления, тем легче поварачивать колёса. И по-этому делают "баранку" руля больше, если машина имеет большие колёса.
7) В словесном выражении правило моментов сил звучит следующим образом: Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке равен моменту силы вращающей его против часовой стрелки. Правило моментов сил справедливо для любого тела закрепленного вокруг неподвижной оси. На практике момент силы находят следующим образом: по направлению действия силы проводят линию действия силы. Потом из точки в которой находится ось вращения проводят перпендикуляр до линии действия силы. Длина этого перпендикуляра будет равняться плечу силы. Умножив значение модуля силы на ее плечо получаем значение момента силы относительно оси вращения. То есть мы видим, что момент силы характеризует вращающее действие силы. Действие силы зависит и от самой силы и от ее плеча.
8) Натренированность. - можно так сказать.
9) Думаю что, центр тяжести корабля неизменится.?
Движение тела, брошенного горизонтально или под углом к горизонту.
Движение тела, брошенного горизонтально или под углом к горизонту.
Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
- между координатами квадратичная зависимость, траектория – парабола!
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
Движение тела, брошенного под углом к горизонту.
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория - парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0. Следовательно, для решения этой задачи необходимо решить уравнение . Оно будет иметь решение при t=0 (начало движения) и
Время полета:
Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
- максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
- на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя т.н. навесная и настильная траектории.
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно:
Время подъема: