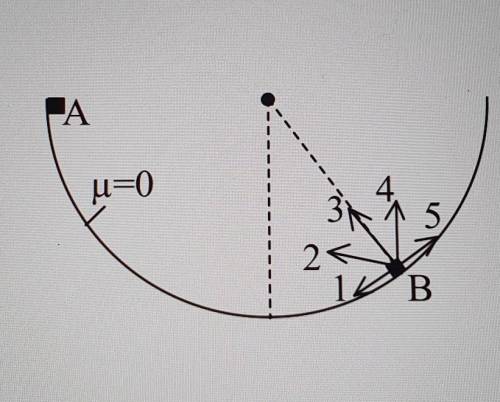
При отсутствии трения малые колебания маятника в вертикальной плоскости происходят по гармоническому закону, причем собственная циклическая частота математического маятника, как известно, зависит только от длины подвеса: ω0=g/l. (1) Вследствие трения колебания маятника будут затухающими: ϕ=ϕe−βtsinωt, где ϕ — угол отклонения нити маятника от вертикали в момент t. (Очевидно, записанный закон движения соответствует такому началу отсчета времени, что при t=0 маятник проходит через положение равновесия, т. е. ϕ=0.) Период затухающих колебаний (период гармонического сомножителя) T=2π/ω=2π/ω02−β2. (2) Амплитудой затухающих колебаний принято считать выражение, стоящее перед гармоническим сомножителем. В соответствии с этим определением амплитуда А затухающих колебаний изменяется со временем по экспоненциальному закону: A(t)=ϕ0e−βt. (3) Записав выражения амплитуды для двух моментов t и t+τ и учитывая, что отношение этих амплитуд задано, можно найти искомое время τ. Число n полных колебаний за это время можно определить, если известен период T. Затухающие колебания по записанному выше закону возникают, как следует из решения соответствующего дифференциального уравнения, только при условии β<ω0 [это очевидно из выражения (2): при β>ω0 период и циклическая частота оказываются мнимыми величинами]. При β≥ω0 происходит апериодический процесс, закон движения которого ϕ=B1e−δ1t+B2e−δ2t, где B1 и B2 — постоянные, определяемые из начальных условий; δ1,2=β±β2−ω02. Запишем выражения (3) для моментов времени t и t+τ: A1=ϕ0e−βt,A2=ϕ0e−β(t+τ). Отношение амплитуд; A1/A2=eβτ=5. Логарифмируя это выражение, находим сτ=ln5/β=1,79с. Число полных колебаний за время τ, очевидно, равно отношению n=τ/T. Определив из выражения (1) собственную циклическую частоту математического маятника и подставив ее в выражение (2), получим сT=1,45с.
1) Пусть время колебаний равно t.
Тогда, в первом случае
T₁ = t / n₁ = t / 26
T₁ = 2π·√ (L₁/g)
Приравняем:
t /26= 2π·√ (L₁/g)
Возведем в квадрат:
t²/ 676 = 4·π²·L / g (1)
2) Аналогично для второго случая. Заметим, что количество колебаний уменьшилось, значит длина нити УВЕЛИЧИЛАСЬ!
T₂ = t / n₂ = t/24
T₂ = 2π·√ (L₁+ΔL)/g)
Приравняем:
t/ 24= 2π·√ (L₁+ΔL)/g
Возведем в квадрат:
t²/576 = 4·π²·(L₁+ΔL) / g (2)
3) Разделив (2) на (1), получаем:
1 + ΔL / L₁ = 676 / 576
ΔL / L₁ = 1,174 - 1
ΔL / L₁ = 0,174
L₁ = ΔL / 0,174 = 0,05 / 0,174 ≈ 0,29 м или 29 см