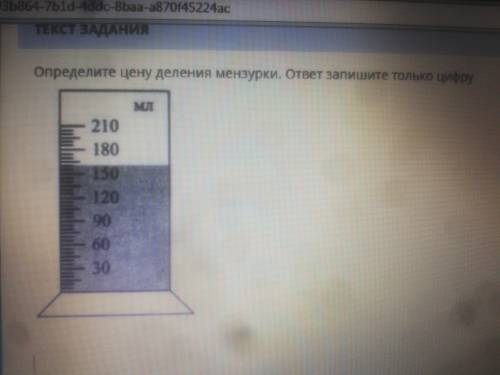

0,26 В
5 В
Объяснение:
Получился делитель напряжения, подключая вольтметр к 10 резисторам мы невольно ожидаем что он покажет половину напряжения батареи, то есть 2,75 В, но он показывает меньше. В чем же причина? Причина в вольтметре - он не идеален, т.е. его сопротивление не бесконечно. Будем решать задачу с этой позиции.
Напряжение, которое показывает вольтметр в первом случае (R' - сопротивление самого вольтметра)
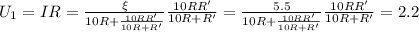
Выразим отсюда сопротивление вольтметра R', так как выражение весьма неудобочитаемо, заменим дробь, ответственную за сопротивление ветви резистор/вольтметр, на х и найдем его

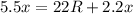
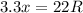
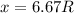
Вернемся к нашей замене и выразим R'
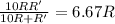
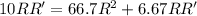
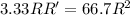
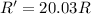
Сопротивление вольтметра нашли.
Теперь подключим его параллельно одному резистору, он покажет напряжение
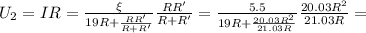
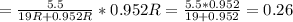 В
В
Подключим вольтметр к 19 резисторам
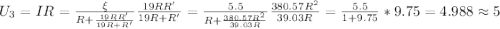 В.
В.

W = mgh.
При малых смещениях можно считать, что амплитуда колебаний по дуге желоба l равна проекции этой дуги на горизонталь X0. Из прямоугольного треугольника, образованного радиусом желоба R, амплитуды горизонтального смещения X0 и проекции крайнего положения шарика на вертикаль (R-h) следует:
X0^2 + (R-h)^2 = R^2
Отсюда получим: X0^2 = 2*R*h - h^2
Учитывая, что при малых колебаниях h^2 << 2*R*h
X0^2 = 2*R*h
Таким образом, получаем выражение для h через амплитуду X0 при малых отклонениях от положения равновесия:
h = X0^2/2R
Потенциальная энергия, максимальная при крайнем положении шарика обретает вид:
W = m*g*X0^2/2R
Теперь получим значение максимальной кинетической энергии шарика (при прохождении положения равновесия). Она равна:
T = m*V0^2/2 + I*Omega^2/2
поскольку, коль шарик катится по жёлобу без проскалзывания, мы должны, помимо кин энергии поступательного движения шарика массы m, учитывать ещё и энергию вращения шарика с моментом инерции I и угловой скоростью вращения шарика вокруг его собственной оси Omega.
При этом максимальная линейная скорость шарика
V0 = Omega*r, где r = радиус шарика =>
Omega = V0/r
T = m*V0^2/2 + I*(V0/r)^2/2
Если шарик совершает гармонические колебания по закону
x(t) = X0*Sin(omega*t) то его скорость должна меняться по закону
v(t) = x'(t) = omega*X0*Cos(omega*t)
Таким образом, максимальная линейная скорость шарика (амплитуда скорости) равна
V0 = omega*X0, где omega - циклическая частота колебаний шарика.
Выражение для максимальной кинетической энергии шарика принимает вид:
T = m*(omega*X0)^2/2 + I*(omega*X0)^2/(2r^2).
Поскольку момент инерции шарика радиуса r и массы m равен
I = (2/5)mr^2, то
T = m*(omega*X0)^2/2 + (2/5)mr^2*(omega*X0)^2/(2r^2) = (7/10)m*(omega*X0)^2
В колебательной системе максимальное значение потенциальной энергии W равно максимальной величине кинетической энергии T.
(7/10)m*(omega*X0)^2 = m*g*X0^2/2R
отсюда, сокращая в обеих частях равенства m и X0 получаем:
(7/5)*omega^2 = g/R
и окончательно
omega^2 = (5/7)*(g/R)
и
omega = sqrt(5g/7R).
Частота такого "маятника" niu = omega/2Pi
niu = sqrt(5g/7R)/2Pi
Период T = 1/niu = 2Pi*sqrt(7R/5g)