Дано:
t1 = 0,9 c
t2 = 1,2 c
g = 10 м/с²
h, υ0 - ?
Если вычесть из t2 время t1, то получим t3 - время, которое было затрачено телом на подъём с высоты h на максимальную высоту и спуск с неё обратно на высоту h:
t3 = t2 - t1
Время на подъём и время на спуск равны:
tп = tс = t3/2
На максимальной высоте скорость тела υ' обращается в нуль, тогда выразим скорость тела на высоте h, приняв её за υ0':
υ' = υ0' - gtп
υ' = 0 => υ0' = gtп = g*t3/2 = g*(t2 - t1)/2
Теперь выразим υ0, подставив вместо υ = υ0' его выражение:
υ = υ0' = υ0 - gt1
g*(t2 - t1)/2 = υ0 - gt1
υ0 = g*(t2 - t1)/2 + gt1 = g*(t2/2 - t1/2 + t1) = 10*(1,2/2 - 0,9/2 + 0,9) = 10*(0,6 - 0,45 + 0,9) = 10*1,05 = 10,5 м/с
h = υ0t1 - gt1²/2 = 10,5*0,9 - 10*0,9²/2 = 5,4 м
h = υ0t2 - gt2²/2 = 10,5*1,2 - 10*1,2²/2 = 5,4 м
ответ: 10,5 м/с, 5,4 м.
Объяснение:
1. Найдем емкостное сопротивление Xc:
Xc=1/(2πfC), где
f - заданная частота сети, Гц;
С - емкость конденсатора, Ф;
π - число "Pi"
Xc=1/(2*3.14*50*100*10⁻⁶)=31.8 (Ом)
2. Найдем полное сопротивление второй ветви Z₂:
Z₂=√(R₂²+(XL-Xc)²);
Z₂=√(15²+31.8²)=35 (Ом)
3. Найдем угол сдвига между активной и емкостной составляющей сопротивления Z₂:
tg φ=Xc/R₂; tg φ=31.8/15=2.12; φ=arctg 2.12≈65°;
4. Найдем величину (модуль) напряжения U:
U=I₁*R₁; U=2.5*30=75 (В)
5. Найдем величину (модуль) тока во второй ветви I₂:
I₂=U/Z₂; I₂=75/35=2.1 (A)
6. Найдем сумму токов первой и второй ветви I₁ + I₂:
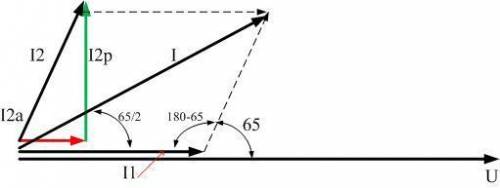
т.к. во второй ветви ток I₂ сдвинут по фазе относительно напряжения (а значит и тока I₁, т.к. ток I₁ совпадает по фазе с напряжением U) на угол ≈65°, то сумму токов I₁ + I₂ будем искать, как векторную сумму.
Применим теорему косинусов (учтя, что угол между векторами токов при сложении по правилу паралеллограмма равен 180-φ. См. Векторную Диаграмму).
I=√(I₁²+I₂²-2*I₁*I₂*cos (180-φ));
I=√(2.5²+2.1²-2*2.5*2.1*cos(180-65)=√(6.25+4.41-10*(-0.42)=3.85 (А)
7. Показания ваттметра.
Смотрим на ВД. Угол между общим током I и напряжением U равен (опять из паралеллограмма) φ/2
P=U*I=cos φ; P=75*3.85*cos(65/2)°=243 (Вт)
8. Строим Векторную Диаграмму:
I₁=2.5 A
активная составляющая ток второй ветви:
I₂_a=2.1*cos 65=0.89 A
реактивная (емкостная) составляющая тока второй ветви:
I₂_p=2.1*sin 65=1.9 A
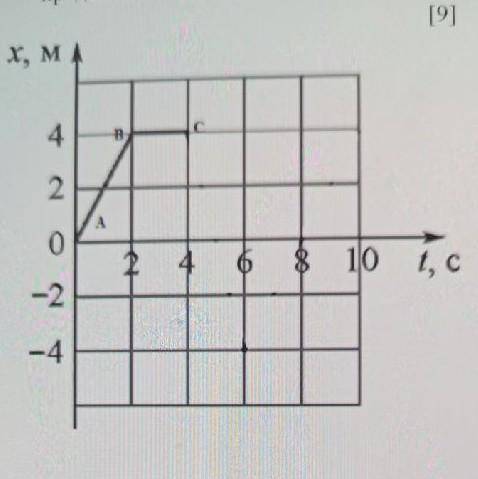
x(t)=4;4
Объяснение: