Численное значение ускорения свободного падения не играет никакой роли. И на Луне и на Марсе время достижения максимальной скорости было бы одинаковым. Отличалась бы только сама эта максимальная скорость. Поскольку, как хорошо известно, частота пружинных колебаний в продольном однородном потенциальном поле происходят с той же частотой, что и в его отсутствии. Каждую четверть периода гармонических колебаний – модуль скорости меняет своё значение от нулевого до амплитудного и наоборот.
БЕЗ ДОКАЗАТЕЛЬСТВА ФАКТА НЕИЗМЕННОМТИ ПЕРИОДА КОЛЕБАНИЙ:
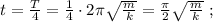
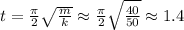сек ;
ВТОРОЙ с доказательством неизменности периода:
Будем для начала откладывать координату вниз от начального положения груза. На груз всё время будет действовать сила:
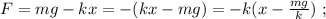
Теперь станем откладывать координату от точки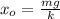 
и получим смещённую координату:
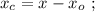и теперь уже можем записать уравнение для силы так:
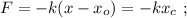
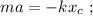
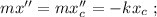
Последнее – это уравнение гармонических колебаний с циклической частотой:
и периодом:
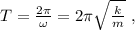нас интересует четверть-период, так что:
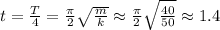сек ;
ТРЕТИЙ с доказательством неизменности периода:
На груз всё время будет действовать сила:
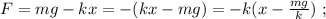
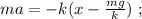
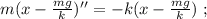
Это уравнение гармонических колебаний с циклической частотой:
и периодом:
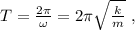нас интересует четверть-период, так что:
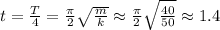сек ;
ЧЕТВЁРТЫЙ с доказательством неизменности периода:
Будем откладывать координату вниз от начального положения груза. По закону сохранения энергии:
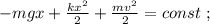
Возьмём производную от обеих частей уравнения:
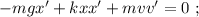
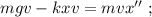
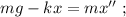
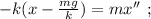
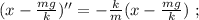
Это уравнение гармонических колебаний с циклической частотой:
и периодом:
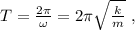нас интересует четверть-период, так что:
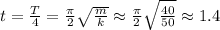сек .
Если сжимать воду при комнатной температуре, она останется жидкой до давления порядка 1 ГПа, при котором её плотность будет порядка 1.2 г/см3. То есть мы увеличим плотность на 20% или, если хотите, уменьшим объем на 1/6.
При более высоких давлениях жидкой фазы не будет, появятся последовательно лед-VI, лед-VII, лед-X. Дальше экспериментальных данных, насколько мне известно, нет, только расчёты (там тоже много чего интересного ожидается, но пока забудем). Лёд-X при 128 ГПа имеет плотность порядка 3.5 г/см3. Такой лёд уже получается тяжелее, например, гранита.