Задача решена через моменты сил. Сила натяжения Т2 стремится повернуть блок относительно его оси против часовой стрелки. А сила Т1 - по часовой. Здесь важно понять, что на самом деле сила Т2 не поворачивает блок влево - ведь блок крутится вправо под действием силы m2g. Просто мысленно прикидывается: а куда бы повернула сила Т2 этот блок, если бы она оказала решающее действие на него относительно его оси. Это просто нужно для определения знака момента. Если сила стремится повернуть тело против часовой, то её момент принято считать положительным. Это сделано для удобства по аналогии с тригонометрическим кругом (отсчёт углов против часовой стрелки является положительным). Ведь есть задачи, в которых момент силы не такой очевидный как в этой: там плечо силы может высчитываться с синуса или косинуса.
Поэтому у Т2 знак "плюс", а у Т1 - "минус".
1.
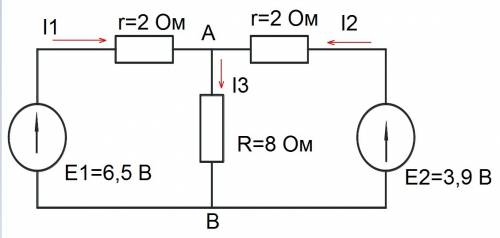
Схема, эквивалентная описанной цепи, приведена в приложении 1.
Проанализировав данную схему, нетрудно заметить, что в ней только два узла. В связи с этим, наиболее рациональным методом решения представляется метод двух узлов, являющийся частным случаем метода узловых потенциалов.
Напряжение между точками A и B может быть определено по формуле:
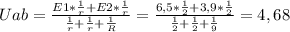 В
В
Тогда токи:
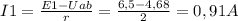
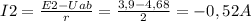
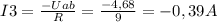
Знак минус указывает на то, что в действительности ток течет в направлении, противоположном указанному стрелкой на схеме.
2.
Схема, эквивалентная описанной цепи, приведена в приложении 2.
Ток может быть найдем по закону Ома:
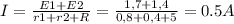
Тогда напряжение на внешней цепи:
U = I*R = 0,5*5 = 2,5 В
Напряжения на зажимах элементов (учитывая падение напряжения на внутреннем сопротивлении):
U1 = E1-I*r1 = 1,7-0,5*0,8 = 1,3 В
U2 = E2-I*r2 = 1,4-0,5*0,4 = 1,2 В
ответ 200
Объяснение:
100:0,5=200