Объяснение:
№1
P = IU = I²R
P1/P2 = ( ( 2I )²( R/4 ) )/( I²R ) = ( I²R )/( I²R ) = 1
№2
η = Рпол./Рзат. * 100%
η = ( I2U2 )/( I1U1 ) 100%
I1 = ( I2U2 )/( ηU1 ) 100%
I1 = ( 9 * 22 )/( 90% * 220 ) 100% = 1 A
№3
λ = Тv
λ = 2π√( LCоб. )v
λ = 2π√( L( C1 + C2 ) )v
λ = 2 * 3,14 √( 10 * 10^-3 ( 360 * 10^-12 + 40 * 10^-12 ) ) 3 * 10^8 = 2 * 3,14 √( 10^-2 ( ( 36 + 4 ) 10^-11 ) 3 * 10^8 = 3768 м
№4
WC( max ) = ( CU( max )² )/2
WL( max ) = ( LI( max )² )/2
W = WC( max ) = WL( max )
( CU( max )² )/2 = ( LI( max )² )/2
CU( max )² = LI( max )²
С = ( LI( max )² )/( U( max )² )
W = WC + WL
W = ( CU² )/2 + ( LI² )/2
( CU( max )² )/2 = ( CU² )/2 + ( LI² )/2
CU( max )² = CU² + LI²
LI( max )² = ( LI( max )²U² )/U( max )² + LI²
LI( max )² = L ( I( max )²U² )/U( max )² + I² )
I( max )² = ( I( max )²U² )/U( max )² + I²
Подставим численные данные и решим уравнение
( 5 * 10^-3 )² = ( ( 5 * 10^-3 )²U²/2² ) + ( 3 * 10^-3 )²
2,5 * 10^-5 = 6,25 * 10^-6U² + 9 * 10^-6
( 25 - 9 ) 10^-6 = 6,25 * 10^-6U²
16 = 6,25U²
U = √( 16/6,25 ) = 1,6 B
Человек, рост которого составляет h = 189 см, стоит под фонарём. Его тень при этом составляет L° = 170 см. Если он отойдёт от фонаря ещё на x = 0,18 м = 18 см, то его тень станет равна L” = 206 см. На какой высоте над землёй висит фонарь?
Чёрный треугольник: Н/h = AD/L° = AD/170; (*)
Красный треугольник: Н/h = AC/L” = AC/206. (**)
Но DС = L”+ x – L° = 206 + 18 – 170 = 54 см. (***)
Делим (**) на (*): 1 = (АС/206)/(AD/170), откуда: (АС/206) = (AD/170) или:
АС = 1,21*AD.
Но из (***): DC = 54 см. Или AC – AD = 54. ==> 1,21*AD – AD = 54 ==> 0,21*AD = 54 ==> AD = 257,1 см.
Подставив AD в (*), получим: 170*H = h*AD ==> H = h*257,1/170 = 189*257,1/170 = 285.8 см.
Итак, фонарь висит на высоте Н = 286 см.
Объяснение:
По формуле электролиза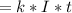
, где k - электрохимический эквивалент (для серебра k = 1,118*10⁻⁶ кг/Кл), t - промежёток времени (с), I - действующая сила тока (А). В системе СИ: 15 мин = 900 с. Подставляем численные данные и вычисляем: 