Интересная задача
Дано:
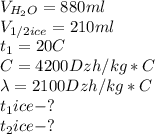
Для начала вспомним закон сохранения мас. Масса неизменная при переходе телом из одного агрегатного состояния в другое.
Поэтому мы может высчитать масу снега в термосе.
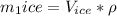
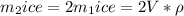
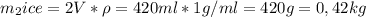
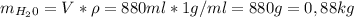
Мы нашли масу снега, поэтому подставим в уравнение теплового баланса
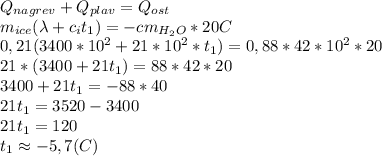
Минус появился, поскольку мы решали только арифметику, и не учитывали, кто теплоту отдает.
Второй вопрос можно решить логически. По сути у нас удельная теплоемкость льда в два раза меньше, а массу при этом мы берем вдвое больше, поэтому можно будет поделить обе части на эту теплоемкость и получится:
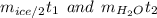
Очевидно, что масса снега меньше, чем воды (примерно в 4 раза), если подставить температуру 20 в правую часть, то при сравнении будет знак <, то бишь у воды еще останется запас теплоты.
Но на плавление льда её не хватит, поскольку лямбда намного больше чем. 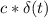
№1.
По формуле мощности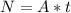 , где A - работа (Дж), t - промежуток времени (с). Работа совершаемая при этом есть произведение перемещения к действующей силе при этом т.е.
, где A - работа (Дж), t - промежуток времени (с). Работа совершаемая при этом есть произведение перемещения к действующей силе при этом т.е. 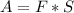 , где S - перемещение тела (м), F - действующая сила при этом (Н).
, где S - перемещение тела (м), F - действующая сила при этом (Н).
Подставив данную формулу в формулу мощности получим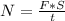 . Подставляем и вычисляем:
. Подставляем и вычисляем: 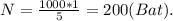
№2.
По безвременной формулы скорости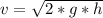 , где h - перемещение (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставив получим
, где h - перемещение (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставив получим 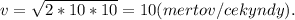 . Если развиваемая скорость во время падения равна 10 м/с - это 100%, а после удара о землю имеетскорость х - это 30%, то составляя пропорцию получаем
. Если развиваемая скорость во время падения равна 10 м/с - это 100%, а после удара о землю имеетскорость х - это 30%, то составляя пропорцию получаем 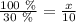 отсюда
отсюда 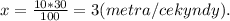 скорость которую потерял мяч при ударе о землю. Тогда скорость движения после удара о землю будет
скорость которую потерял мяч при ударе о землю. Тогда скорость движения после удара о землю будет 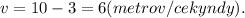
Тогда высота на которую отскочит мяч определяется по формуле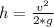 - формулы выведена из безвременной формулы скорости.
- формулы выведена из безвременной формулы скорости.
Подставляем численные данные и вычисляем: