90
Объяснение:
Тебе нужно найти коэффициент преобразования шкалы Гения в шкалу Цельсия, т.к. очевидно, что соотношение не линейное.
Для этого берем Δ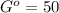 и Δ
и Δ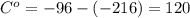
Соответственно, 50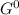 = 120
= 120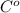
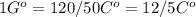
Далее, берем дельту между 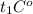 и
и 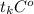 = 216, и делим на полученный коэффициент 12/5
= 216, и делим на полученный коэффициент 12/5
Получаем 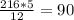
ответ: скорость, с которой рассчитывал ехать водитель 80км/час.
Водитель опоздал на 45 минут.
Объяснение: Для нахождения скорости, с которой собирался проехать водитель, необходимо расстояние между городами разделить на время движения: V=S:t=400:5=80км/час. Четверть пути, которое водитель ехал со скорость 50км/час составляет: 400:4=100км. Время, затраченное на это расстояние равно: 100:50=2часа. Путь, который проехал водитель со скоростью 80км/час равен: 400-100=300км. Время, затраченное на 300км со скоростью 80 км/час равно:
300:80=3,75часа=3час 45мин. Все время в пути автобуса будет
3,75 + 2=5,75час. или 5час 45мин - 5 час = 45 мин - на столько времени опоздал водитель.
C осью времени, похоже, немного напутали. Графики - прямые, тогда после 5-ки должна идти 7-ка. Ну или перед 5-кой должна стоять 4-ка.
Нужно найти начальные координаты тел, графики перемещения которых изображены в осях Х и t.
Графики - прямые. Значит, движения тел равномерное. График третьего тела параллелен оси времени, значит тело стоит на месте - его начальная координата 20 м не изменяется с течением времени. Начальные координаты 1-го и 3-го:
х0_1 = 30 м
х0_3 = 10 м
Скорость определим как отношение пути к затраченному на этот путь времени:
υ = S/t
Возьмём точку пересечения графиков 3 и 1 и найдём скорость первого тела. За 5 секунд оно расстояние, равное разности координаты в момент времени 5 с и начальной координаты:
υ1 = S/t = (x(t) - x0_1)/t = (20 - 10)/5 = 2 м/с
Т.к. разность координат положительна, то проекция скорости тоже положительна, она направлена по оси Х.
Скорость третьего тела равна нулю, т.к. тело не движется:
υ3 = 0
Нулевой вектор направлен во все стороны. Значит скорость третьего тела направлена во все стороны - поэтому оно и не движется.
Второе тело движется против оси Х, значит его скорость тоже направлена против оси. Проекция скорости будет иметь знак "минус". Возьмём точку пересечения графиков 3 и 2:
υ2 = S/t = (x(t) - x0_2)/t = (20 - 30)/3 = -10/3 = -3,3 м/с
Уравнения:
x1(t) = x0_1 + υ1*t
x1(t) = 10 + 2*t
x3(t) = x0_3 + υ3*t
x3(t) = 20 + 0*t = 20
x2(t) = x0_2 + υ2*t
x2(t) = 30 + (-10/3)*t = 30 - (10/3)*t
ответ будет 60
Вот:
1) Определяем величину одного градуса Гения по сравнению с градусом Цельсия. Для этого интервал в градусах Цельсия делим на соответствующий интервал в градусах Гения. Полученный результат обозначаем за . Получаем:
1 °=2°−1°2°−1°=(−16−−82)(30−0)=2,2 °=.
2) Определяем разницу в градусах Цельсия между данной температурой в градусах Цельсия и температурой плавления парафина. Сравниваем температуру плавления с данной температурой в градусах Цельсия 1°, которая равна −82 °. Разница Δ°=°−1°=50−(−82)=132 °.
3) Переводим разницу в градусах Цельсия Δ° в разницу в градусах Гения Δ°, здесь используем полученное в первом пункте значение градуса Гения по сравнению с градусом Цельсия:
Δ°=Δ°=1322,2=60 °.
4) Разницу температур в градусах Гения Δ° прибавляем к данному значению температуры в градусах Гения 1° и получаем ответ °:
°=1°+Δ°=0+60=60 °.
По новой шкале Гения температура плавления парафина равна 60