Для решения этой задачи мы можем использовать закон Вина, который устанавливает зависимость между максимумом спектра испускания черного тела и его температурой.
Закон Вина можно записать следующим образом:
λ_max * T = k,
где λ_max - длина волны, соответствующая максимуму спектра испускания, T - температура черного тела в градусах Кельвина, k - постоянная Вина.
В данной задаче нам дана температура черного тела, равная 37 градусов по Цельсию. Чтобы перевести ее в Кельвины, мы должны добавить 273 к значению температуры: T = 37 + 273 = 310 Кельвинов.
Теперь мы можем использовать закон Вина для определения длины волны отвечающей максимуму испускания:
λ_max * 310 = k.
Зная, что постоянная Вина k равна приблизительно 2.898 * 10^(-3) м * Кельвин, мы можем решить уравнение относительно λ_max:
λ_max = k / 310.
Подставляя значение постоянной Вина, получаем:
λ_max ≈ (2.898 * 10^(-3) м * Кельвин) / 310 ≈ 9.354 * 10^(-6) метров.
Таким образом, длина волны отвечающая максимуму испускания черного тела при температуре 37 градусов по Цельсию составляет примерно 9.354 * 10^(-6) метров.
Теперь перейдем к второй части задачи - определению энергетической светимости черного тела.
Энергетическая светимость черного тела определяется по формуле Планка:
E = σ * T^4,
где E - энергетическая светимость черного тела, σ - постоянная Планка, T - температура черного тела в Кельвинах.
Значение постоянной Планка σ равно приблизительно 5.67 * 10^(-8) Вт/(м^2 * К^4). Таким образом, для определения энергетической светимости мы можем использовать формулу:
Пусть движение происходит вдоль оси z, а 0 находится на уровне земли.
Тогда уравнение движения первого тела: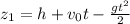 , его скорость:
, его скорость: 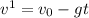
уравнение движения второго тела: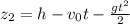
Пусть первое тело достигло максимальной высоты в момент времени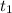 . В этот момент его скорость равна
. В этот момент его скорость равна  . Или
. Или 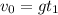
Подставим значение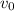 в уравнение движения первого тела в момент времени
в уравнение движения первого тела в момент времени 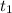 , которое в этот момент находилось на высоте Н:
, которое в этот момент находилось на высоте Н:
и в уравнение для второго, которое находилось на земле: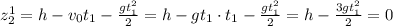 . Или
. Или 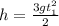
Из уравнения для первого тела: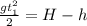 подставим в уравнение для второго:
подставим в уравнение для второго: 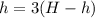 .
.
Получаем: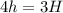 . Тогда:
. Тогда: 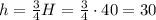 м.
м.
Найдем начальную скорость из выражения: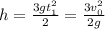 .
.
Получаем: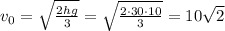 м/с.
м/с.