Наклонная плоскость является одним из простых механизмов. Она позволяет поднимать груз вверх, прикладывая к нему усилие, заметно меньшее, чем сила тяжести, действующая на этот груз
Объяснение:
.
Дано:
L = 200 м
v = 5 м/с
v' = 3 м/с
V, t, β, s - ?
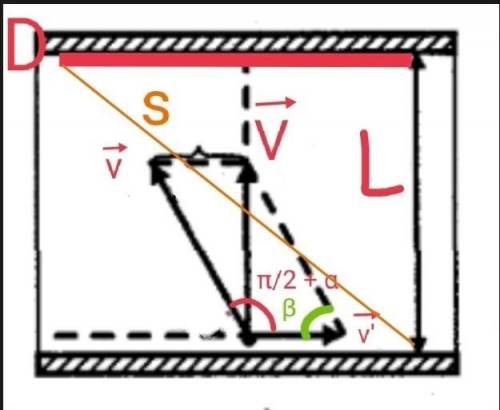
Кратчайший путь - это путь, перпендикулярный берегам реки. В таком случае лодка должна противодействовать течению реки, чтобы её не сносило в сторону, когда она поплывёт перпендикулярно берегам. Ведь если она не будет противодействовать, то путь окажется не перпендикулярным, а диагональным. Получается, что cкорость лодки должна быть направлена под тупым углом (π/2 + α) к направлению скорости течения и, следовательно, к берегу, от которого лодка движется, т.к. течение реки происходит параллельно этому берегу. Сделаем расклад скорости лодки на вертикальную составляющую и горизонтальную составляющую. У нас получится прямоугольный треугольник, в котором гипотенуза - это скорость лодки относительно воды v, катет, параллельный берегу, - скорость течения v', и катет, перпендикулярный берегу, - скорость лодки относительно берега V. Угол β - острый угол между скоростью v и берегом, который нам и нужно будет найти. Выходит, что скорость относительно берега равна геометрической разности скорости относительно воды и скорости течения:
V² = v² - v'² = 5² - 3² = 25 - 9 = 16 => V = 4 м/с.
Найдём время:
t = L/V = 200/4 = 50 c
Найдём угол β между направлением скорости лодки v и берегом из соотношения катетов прямоугольного треугольника - поделим скорость V (противолежащий катет) на скорость v' (прилежащий катет):
tgβ = V/v' = 4/3 - теперь найдём арктангенс: β = arctg(4/3) = 59,033 = 59°
Остаётся найти перемещение лодки относительно воды. Т.к. горизонтальная составляющая скорости лодки относительно воды v по модулю равна скорости течения v', то абсолютная скорость лодки в системе отсчёта "вода" равна этой же скорости:
Vabs = |v'| = v' = 3 м/с
За время t лодка переместится относительно воды по горизонтали на расстояние:
D = Vabs*t = 3*50 = 150 м
По вертикали лодка переместится на расстояние L, тогда полное перемещение лодки s будет равно геометрической сумме L и D:
s² = L² + D² = 200² + 150² = 40000 + 22500 = 62500 => s = √62500 = 250 м
ответ: 4 м/с, 50 с, 59°, 250 м.
Объяснение:
№1
Дано:
а=60 см; в=40 см; h=10 см; h2=1,5 м; p(плотность)=1600кг/м3; g=9,8H/кг
А=?
Си:
0,6 м; 0,4 м; 0,1 м
Формулы:
А=Fh2; F=mg; m=pV; V=авh
V=0,6м*0,4м*0,1м=0,024м3
m=1600кг/м3*0,024м3=38,4кг
F=38,4кг*9,8Н/кг=384Н
А=384Н*1,5м=576Дж
ответ: 576Дж
№2
Дано:
t=20 мин; S=30км; F=2,4кН
N=?
Си:
1200 сек; 30000 м; 2400Н
Формулы:
N=A/t
A=FS
А=2400Н*30000м=72000000Дж
N=72000000Дж/1200сек=60000Вт=60МВт
ответ: 60 МВт
№3
Дано:
m=0,5кг; V=10м/с
Ек=?
Формулы:
Ек=mV^2/2
^2V=v*v
v^2=10м/с*10м/с=100м^2/c^2
Ек=0,5кг*100м^2/c^2/2=25Дж
ответ: 25Дж
№4
Дано:
Еп=12Дж; m=0,4кг; g=9,8м/с2
h=?
Формулы:
h=Еп/mg
h=12дж/0,4кг*10м/с2=3м
ответ: 3м
№5
Дано:
m=300г; Ек=30Дж
V=?
Си:
0,3кг
Формулы:
V=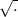 2Ек/m
2Ек/m
V=2*30Дж/0,3кг=14,14м/с
ответ: 14,14м/с
Наклонная плоскость является простым механизмом, который используют для того, чтобы сэкономить силу при вертикальном перемещении различных грузов. Наклонные плоскости имеются на всех въездах наверх, например, на въездах на мост или на многоэтажную автостоянку.
Объяснение: