Решение. Из w = mв-ва / mр-ра находим массу хлорида натрия:
mв-ва = w • mр-ра = 0,1 • 250 г = 25 г NaCl
Поскольку mр-ра = mв-ва + mр-ля, то получаем:
m(Н20) = mр-ра — mв-ва = 250 г — 25 г = 225 г Н20.
Задача 3.2. Определите массу хлороводорода в 400 мл раствора соляной кислоты с массовой долей 0,262 и плотностью 1,13 г/мл.
Решение. Поскольку w = mв-ва / (V • ρ), то получаем:
mв-ва = w • V • ρ = 0,262 • 400 мл • 1,13 г/мл = 118 г
Задача 3.3. К 200 г 14%-ного раствора соли добавили 80 г воды. Определите массовую долю соли в полученном растворе.
Решение. Находим массу соли в исходном растворе:
mсоли = w • mр-ра = 0,14 • 200 г = 28 г.
Эта же масса соли осталась и в новом растворе. Находим массу нового раствора:
mр-ра = 200 г + 80 г = 280 г.
Находим массовую долю соли в полученном растворе:
w = mсоли / mр-ра = 28 г / 280 г = 0,100.
Объяснение:
m⋅a⃗ c=F⃗ 1+F⃗ 2+...(1)
где ac = ω2∙R — центростремительное ускорение тел, R = l + Δl — радиус вращения, l — начальная длина пружины и резинки, Δl — их удлинение, ω = 2π∙ν — угловая скорость вращения, ν = N/t — частота вращения, N — число оборотов за время t.
На все тела действует сила упругости, т. е. F1 = Fy = k∙Δl, k — коэффициент жесткости пружины или резинки. Разберемся с остальными силами, действующими на тела.
На грузик действует только сила упругости резинки (Fy), т. к. по условию «силой тяжести грузика пренебречь». Тогда рисунок можно сделать для любого положения грузика (рис. 4). Запишем проекцию уравнения (1) на ось 0Y:
m∙ac = Fy (3)
С учетом пояснений к (1), уравнения (2) и (3) примут вид:
m⋅ω2⋅R=k⋅Δl,m⋅(2π⋅Nt)2⋅(l+Δl)=k⋅Δl.
По условию l = 30 см = 0,3 м, m = 8 г = 0,008 кг, N = 120, t = 1 мин = 60 с, Δl = 10 см = 0,1 м. Тогда
k=(2π⋅Nt)2⋅m⋅(l+Δl)Δl,
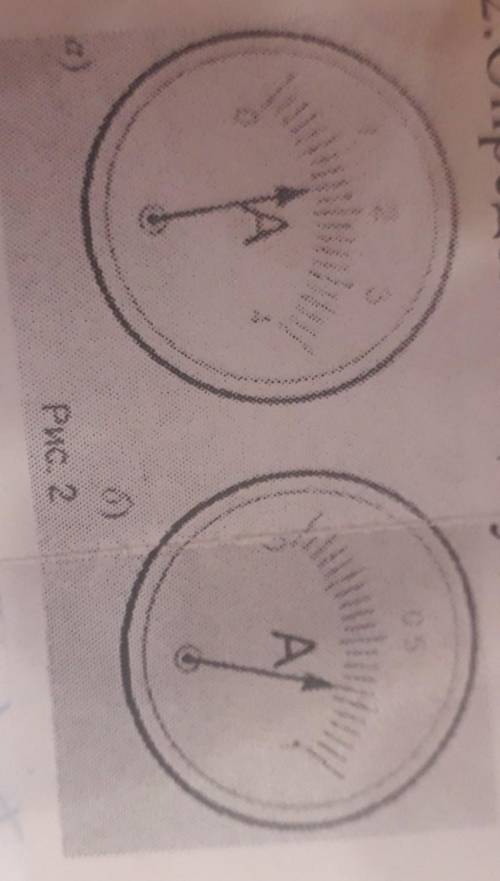
1.6A
0.7A
второй, цена деления меньше
Объяснение: