) и расписать суммарную силу давления (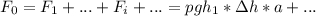
), то мы получим, что эта сила ровно вдвое меньше, чем если бы на всю стенку дествовало такое же давление, как у дна. Следовательно, если мы хотим ввести некое "среднее давление" на эту стенку, оказывающее то же действие, что и реальное давление, оно должно быть вдвое меньше, чем давление на дно.
F1=k*(q1*Q1)/r1^2
F2=k*(q2*Q2)/r2^2
q2=2*q1
Q2=2*Q1
r2=4*r1
F2=k*(q2*Q2)/r2^2=k*(2*q1*2*Q1)/(4*r1)^2=k*(q1*Q1)/(r1)^2*1/4
F2/F1=k*(q1*Q1)/(r1)^2*1/4 : k*(q1*Q1)/(r1)^2 = 1/4
ответ - сила уменьшится в 4 раза