Объяснение:
два тела имеют скорости и массы в исходной системе координат
m1 m2 v1 v2
координата центра масс ищется как х_цм =(m1*x1+m2*x2)/(m1+m2)
скорость центра масс v_цм = (m1*v1+m2*v2)/(m1+m2)
в нашем случае v_цм = (m1*v1+m2*v2)/(m1+m2) = (0,3*1+0,1*0)/(0,3+0,1) = 0,75
итак, первая тележка движется со скоростью 1 м/с и приближается к центру масс со скоростью (1-0,75) м/с = 0,25 м/с
итак, вторая тележка движется со скоростью 0 м/с и приближается к центру масс со скоростью (0-0,75) м/с = -0,75 м/с
после упругого столкновения скорости тележек относительно центра масс просто поменяют знак
(при неупругом столкновении они бы просто стали бы равны нулю)
итак
после упругого столкновения
скорость первой тележки относительно центра масс стала равна -0,25 м/с , а в исходной системе отсчета -0,25+0,75 = 0,5 м/с - это ответ
скорость второй тележки относительно центра масс стала равна 0,75 м/с , а в исходной системе отсчета 0,75+0,75 = 1,5 м/с - это ответ
***************************************************
ответ 0,5 м/с и 1,5 м/с (направление движения обеих тележек совпадает с первоначальным направлением движения первой тележки)
****************************************************************************************
можно было воспользоваться готовыми формулами смотри вложение
основанными на решении типовой задачи где применяются законы сохранения и импульса
переписывать вывод формул из учебника или из интернета не вижу смысла - процесс неинтересный
результат на картинке
u1=((m1-m2)*v1+2m2v2)/(m1+m2)=((0,3-0,1)*1+2*0,1*0)/(0,3+0,1)=0,5 м/с
u2=((m2-m1)*v2+2m1v1)/(m1+m2)=((0,1-0,3)*0+2*0,3*1)/(0,3+0,1)=1,5 м/с
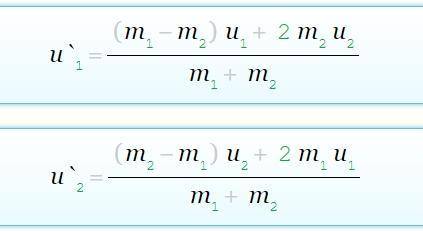
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
Взаимное расположение прямых и их направляющие векторы
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
l_{1}\colon~\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}, \quad l_{2}\colon~\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}\,.