Для решения используем формулу истечения жидкости при опорожнении открытого в атмосферу сосуда произвольной формы через донное отверстие.
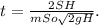
Таким образом, время полного опорожнения резервуара, с постоянным сечением по высоте, при постепенном снижении уровня жидкости в два раза больше времени, которое потребовалось бы в случае истечения того же количества жидкости из отверстия под постоянным максимальным напором H.
а) Из этой формулы определяем So:
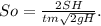
Для отверстия в тонкой стенке m= 0,62. время t = 19*60 = 1140 c.
Подставим данные в формулу:
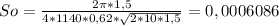 м².
м².
Отсюда находим диаметр выпускного отверстия:
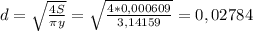 м или примерно 28 мм.
м или примерно 28 мм.
Расход Q определяем из той же формулы, подставив туда значение сечения. Получаем Q = 2,0668 л/с или примерно 2,07 л/с.
б) Время истечения равно t = 2V/Q, где Q - максимальный расход жидкости через отверстие, соответствующий начальному уровню в резервуаре.
Расход Q = 1,5 л/с = 0,0015 м³/с.
t = 2SH/Q = 2*(πD²/4)*H/Q = 2*(3,14159*1²/4)*1,5/0,0015 = 1570,796 с или 26,18 минут.
Если же подставить значение сечения заданного отверстия в формулу для определения времени So = πd²/4 = π*0,025²/4 = 0,0004909 м², то получим результат:
t = 2,3562/(0,62*0,0004909*√(2*10*1,5)) = 1413,478 с или 23,56 минут. Значит, заданный расход в 1,5 л/с не является максимальным расходом жидкости через отверстие, соответствующему начальному уровню в резервуаре.
НАВЕРНОЕ ТОЧНО НЕ ЗНАЮ
Объяснение:
Переведём граммы в килограммы : 10г = 0.01кг
Энегрия пули : K = m* V^2/2
была K = 0,01кг*800м/с*800/2 =3200 дж
стала K = 0,01кг*400м/с*400/2 =800 дж
Работа, затраченная на проход доски = 3200-800 = 2400дж
A = F*S, следовательно
F = A:S = 2400:0.08 = 30000 H
ответ: 30000 Н!