Наверное, в задаче подразумевается, что пробирка заполнена до краев.
Дано:
m1(пробирки с водой) =50г.
m2(с металлом) =60.5г.
m (метала) =12г.
Найти:
p =?
Решение:
V (объем)=50 - (60.5 - 12) = 50 - 48.5 = 1.5 см^3
p =m\V
p =12/1.5 = 8 (г/см^3)
Короче, мы взяли массу пробирки с водой и стали вычитать массу воды после того, как опустили металл, то есть, когда часть воды вылилось (действием в скобках мы вычитали из общей массы воды и металла массу металла, чтобы узнать массу воды после того, как часть металла под выталкиванием металла вылилось).
Объяснение:
Дано :
m1 = 500 г = 0,5 кг
m = 300 г = 0,3 кг
μ = 0,2 кг
g = 10 Н/кг
-----------------------------------
а - ?
Т - ?
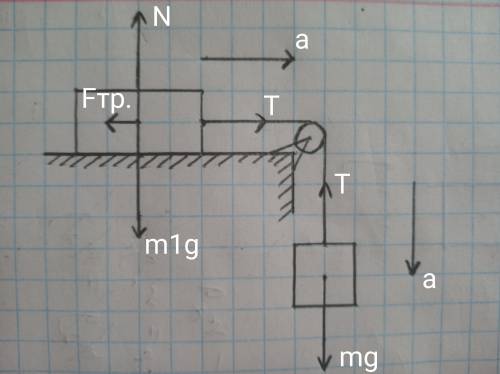
Запишем второй закон Ньютона для обоих тел проекциях на оси
( см. рисунок )
Для тела массой m1
Ox : m1a = T - Fтр.
Оу : 0 = N - m1g
Для тела массой m
Oy : ma = mg - T
Тогда
N = m1g
Мы знаем что
Fтр. = μN
Значит
Fтр. = μm1g
Теперь составив систему уравнений
m1a = T - μm1g
ma = mg - T
Решим систему методом сложения
a ( m + m1 ) = g( m - μm1 )
a = ( g( m - μm1 ) )/( m + m1 ) = 2,5 м/с²
Отсюда
Т = m( g - a )
T = 0,3( 10 - 2,5 ) = 2,25 Н
Вот)
Если достать Ме из воды,то масса оствшейся воды с пробиркой 60,5-12=48,5 (г)
А масса вытесненной металлом воды m=50-48,5=1,5(г)
Значит V вытесненной металлом воды V=m/ро=1,5/1=1,5(см"3)
Плотность P(металла)= m(Me)/V=12/1,5=8(г/см"3)