В совсем строгом смысле - нет (так же, как и падение вблизи поверхности Земли), но с хорошей точностью при небольших высотах его можно считать таковым.
Гравитационную силу, действующую на тело, можно вычислить при формулы
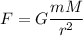 ,
,
где G - некий коэффициент, m - масса тела, M - масса другого тела, r - расстояние между телами.
Считая M - массой Луны, r ≈ R + h, где R - радиус Луны, можно получить выражение для силы:
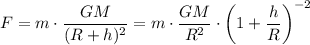
Если h много меньше R (как раз случай падения вблизи поверхности), то последнее слагаемое с хорошей точностью равно 1. Сравнив полученное выражение с F = ma, получаем, что движение равноускоренное с ускорением
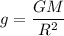
Если рассматривать следующий порядок малости, то g начнёт линейно уменьшаться с ростом h:
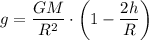
Однако данная поправка будет вносить значимое искажение (скажем, отличие от g у поверхности на 1%) при h = 0.005R, для радиуса Луны это больше 8,5 км.
Поэтому, например, для высот меньше 1 км движение можно считать равноускоренным, тем более, что на Луне атмосфера разреженная и сопротивлением движению можно пренебречь
Дано: U = 220 B; R₀ = 120 Ом
Найти: P₁; P₂; P₃.
Схемы подключения - на рисунке.
1). Схема а. Подключение спиралей последовательное.
Сопротивление плитки: R₁ = 2R₀ = 240 (Ом)
Ток в цепи: I₁ = U/R₁ = 220 : 240 ≈ 0,92 (A)
Мощность плитки: P₁ = I₁U = 0,92 · 220 ≈ 201 2/3 (Вт)
2). Схема б. Одиночное подключение спиралей.
Сопротивление плитки: R₂ = R₀ = 120 (Ом)
Ток в цепи: I₂ = U/R₂ = 220 : 120 ≈ 1,83 (A)
Мощность плитки: P₂ = I₂U = 1,83 · 220 ≈ 403 1/3(Вт)
3). Схема в. Параллельное подключение.
Сопротивление плитки: R₃ = R₀/2 = 120 : 2 = 60 (Ом)
Ток в цепи: I₃ = U/R₃ = 220 : 60 ≈ 3,7 (A)
Мощность плитки: P₃ = I₃U = 3,7 · 220 ≈ 806 2/3 (Вт)
Таким образом: P₁ : P₂ : P₃ = 1 : 2 : 4