На примере рассмотрим свободное падение тела с начальной скоростью
v
0
под действием силы тяжести за промежуток времени
t
. При направлении оси
O
Y
вертикально вниз импульс силы тяжести
F
т
=
mg
, действующий за время
t
, равняется
m
g
t
. Такой импульс равняется изменению импульса тела:
F
т
t
=
m
g
t
=
Δ
p
=
m
(
v
–
v
0
)
, откуда
v
=
v
0
+
g
t
.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала
t
. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы
F
с
р
из временного промежутка
t
. Рисунок
1
.
16
.
2
показывает, каким образом определяется импульс силы, которая зависит от времени.
Изменение импульса
Рисунок
1
.
16
.
2
.
Вычисление импульса силы по графику зависимости
F
(
t
)
Необходимо выбрать на временной оси интервал
Δ
t
, видно, что сила
F
(
t
)
практически неизменна. Импульс силы
F
(
t
)
Δ
t
за промежуток времени
Δ
t
будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на
Δ
t
i
на промежутке от от
0
до
t
, сложить импульсы всех действующих сил из этих промежутков
Δ
t
i
, тогда суммарный импульс силы будет равняться площади образования при ступенчатой и временной осей.
Применив предел
(
Δ
t
i
→
0
)
, можно найти площадь, которая будет ограничиваться графиком
F
(
t
)
и осью
t
. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции
F
(
t
)
из интервала
[
0
;
t
]
.
Рисунок
1
.
16
.
2
показывает импульс силы, находящийся на интервале от
t
1
=
0
с до
t
2
=
10
.
Из формулы получим, что
F
с
р
(
t
2
−
t
1
)
=
1
2
F
m
a
x
(
t
2
−
t
1
)
=
100
Н
⋅
с
=
100
к
г
⋅
м
/
с
.
То есть, из примера видно
F
с
р
=
1
2
F
m
a
x
=
10
Н
.
Объяснение:
1) а = - 0,56 м/с^2
Решение: Переводим скорость и время в СИ. V2 = 20 м/c (*1000:3600) и t = 36 c (*60). Далее воспользуемся формулой ускорения для прямолинейного равноускоренного движения -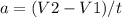 
, где V2 = 20 м/с, а V1 = 0 так как мотоциклист остановился. Подставляем значения и считаем.
2) S = 12,5 м; V1 = 2,5 м/c
Решение: Воспользуемся этой же формулой ускорения - 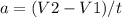, где V2=0, а V1 неизвестно. Выразим V1 
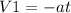. Так как велосипедист тормозит, ускорение направлено против ОХ, то есть равно a = -0,25 м/с^2. Подставляем значения и считаем. Чтобы найти путь, пройденный велосипедистом при торможении воспользуемся формулой связи перемещения тела с его начальной и конечной скорости при прямолинейном равноускоренном движении - 
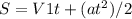. Подставляем значения и считаем.
3) S = 591 м
Решение: Переводим скорость и время в СИ. V1 = 20 м/c (*1000:3600) и t = 30c (*60). Так как автобус тормозит, ускорение направлено против ОХ, то есть равно a = -0,02 м/с^2. Воспользуемся этой же формулой перемещения - 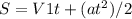. Подставляем значения и считаем.
Процесс плавления происходит при нагреве тела, что вызывает колебания атомов или молекул, из которых состоит тело, внешне это выглядит как плавление, то есть разрушается решетка из которых это тело состоит.
Затвердевание же, наоборот, порисходит из-за потери атомами или молекулами кинетической энергии, под воздействием низких для этого тела температур, т.е. они больше не могут свободно двигаться.