Научные достижения xxi века в мире.(например: нанотехнологии, клонирование и т.п.)

👇

Увидеть ответ

Ответ:

martirosyan01

10.04.2022

плантагон,космос,ретро вирусы

4,5(5 оценок)

Ответ:

немагистор

10.04.2022

Использование нанотехнологий,Обновлённая мобильная связь,Интернет,Небоскрёбы о которых раньше можно было мечтать,Микроволновка,

4,5(57 оценок)

Открыть все ответы

Ответ:

kurmangazievbeka

10.04.2022

57,5 см

Объяснение:

Закон Архимеда:

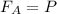F_A = P , где сила Архимеда $F_A = \rho_1gV_1$ , ρ₁ - плотность воды, V₁ - объем погруженной части $\rho_1 S h_2 g= (m_1 + m_2)g$ тела, P - вес тела.

Для одной льдины закон Архимеда:

(1) 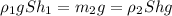$\rho_1 g S h_1 =m_2g = \rho_2 S h g$ , здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.

Отсюда: (2) $h_1 = \frac{\rho_2}{\rho_1}h = \frac{900}{1000}60 = 54$ см

Для льдины с медным кубиком:

(3) 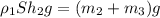$\rho_1 S h_2 g = (m_2+m_3)g$ , m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.

Подставляем сюда вместо m₂ выражение 1, получаем:

(4) 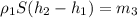$\rho_1 S (h_2-h_1) = m_3$ , где h₂-h₁ =Δh

Теперь запишем закон Архимеда для льдины с железным кубиком:

$\rho_1 S H g = (m_2 + m_4)g$ , m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.

Подставляем сюда выражение 1:

(5) $\rho_1 S H = \rho_1 S h_1 + m_4$ .

Выразим массу железного кубика через массу медного:

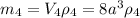$m_4 = V_4\rho_4 = 8a^3\rho_4$ , a - длина ребра куба, ρ₄ - плотность железа.

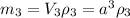$m_3 = V_3 \rho_3 = a^3 \rho_3$ , тогда:

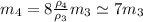
(6) $m_4 = 8 \frac{\rho_4}{\rho_3} m_3 \simeq 7 m_3$

Подставляя (6), (4) в (5):

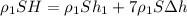
$\rho_1SH = \rho_1Sh_1 + 7\rho_1 S \Delta h$

Упрощая это выражение и подставляя из (2) значение h₁:

$H = h_1 + 7\Delta h = 54 + 7*0.5=57.5$ см.

4,8(48 оценок)

Ответ:

fakersot

10.04.2022

5 с

Объяснение:

Запишем уравнение движения Фокса и Форда, приняв для последнего начальную координату за x₀₂ и скорость за v₂:

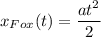
$\displaystyle x_{Fox}(t)=\frac{at^2}{2}$

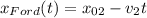
$\displaystyle x_{Ford}(t)=x_{02}-v_2t$

Тогда, расстояние между ними подчиняется закону:

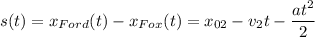
$\displaystyle s(t)=x_{Ford}(t)-x_{Fox}(t)=x_{02}-v_2t-\frac{at^2}{2}$

По условию, в некоторый момент времени τ это расстояние удовлетворяет условию:

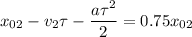
$\displaystyle x_{02}-v_2\tau-\frac{a\tau^2}{2}=0.75x_{02}$

Скорости Фокса и Форда:

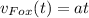
$\displaystyle v_{Fox}(t)=at$

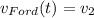
$\displaystyle v_{Ford}(t)=v_2$

Их относительная скорость в момент времени τ:

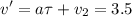$\displaystyle v'=a\tau+v_2=3.5$ м/с

Подставляя все исходные данные в уравнения получим систему:

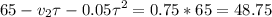
$\displaystyle 65-v_2\tau-0.05\tau^2=0.75*65=48.75$

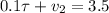
$\displaystyle 0.1\tau+v_2=3.5$

Выражаем скорость Форда из второго уравнения и подставляем ее в в первое:

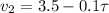
$\displaystyle v_2=3.5-0.1\tau$

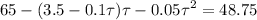
$\displaystyle 65-(3.5-0.1\tau)\tau-0.05\tau^2=48.75$

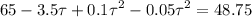
$\displaystyle 65-3.5\tau+0.1\tau^2-0.05\tau^2=48.75$

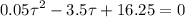
$\displaystyle 0.05\tau^2-3.5\tau+16.25=0$

Решая полученное квадратное уравнение, находим два корня 65 и 5 секунд. Скорости Форда, соответствующие этим временам 3,5-0,1*5=3 м/с и 3,5-0,1*65=-3 м/с, значит нам подходит решение 5 секунд, так как для 65 секунд Форд идет не на встречу Фоксу, а убегает от него.

4,7(93 оценок)

Это интересно:

Образование

21.07.2020

Из разных городов, расстояние между которыми 600 км...

Образование

29.01.2020

Из пункта А в пункт B, расстояние между которыми 84 км...

Хобби-и-рукоделие

21.02.2021

Правила и техника игры в карточную игру Скорость...

Питомцы-и-животные