Решение: A=Fт*h=mgh
Дано:
h= 3м mgh = F*L
L=10м F = mgh/L =580*10*3/10 =1740 Н
m=580кг
g=10 м/с
F - ?
ответ:1740Н
E=200 мВ
Объяснение:
переменная ЭДС, возникающая в контуре при изменении магнитного потока Ф, Вб из-за явления электромагнитной индукции, вычисляется по формуле:
E=dФ/dt, где
Е - величина ЭДС, В
dФ - малое (бесконечно малое) изменение магнитного потока, Вб
dt - малый (бесконечно малый) промежуток времени, с.
Т.к. в условии сказано, что поток изменяется равномерно в течение всего промежутка времени процесса, то перейдем к конечным величинам:
E=ΔФ/Δt;
ΔФ - величина изменения магнитного потока, Вб за конечный промежуток времени Δt, с
Подставим значения:
E=10*10⁻³/(5*10⁻²)=2*10⁻¹ (В)=200 мВ
Рассмотрим уравнения Максвелла в дифференциальной форме, нам понадобятся 3 и 4 уравнения:
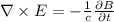
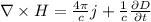
Найдем ротор вектора напряженности по известным его компонентам:
![\nabla \times E=\left[\begin{array}{ccc}i&j&k\\\frac{\partial }{\partial _x} &\frac{\partial }{\partial _y}&\frac{\partial }{\partial _z}\\E_x&E_y&E_z\end{array}\right]=\left[\begin{array}{ccc}i&j&k\\\frac{\partial }{\partial _x} &\frac{\partial }{\partial _y}&\frac{\partial }{\partial _z}\\0&0&cos(y-ct)\end{array}\right] =i*-sin(y-ct)](/tpl/images/1353/9504/213fe.png)
Найдем производную магнитной индукции по времени:
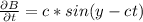
Действительно, легко видеть что они удовлетворяют третьему уравнению.
Теперь найдем ротор вектора напряженности магнитного поля, учитывая что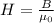 
и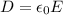 
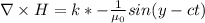
Производная электрической индукции по времени:
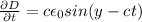
Но так как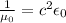 
ротор напряженности магнитного поля также совпадает с производной электрической индукции по времени, деленной на скорость света (для электромагнитной волны плотность тока j считаем нулевой, так как нет среды проводимости).
h= 3м
L=10м
m=580кг
g=10 м/с2
F - ?
решение
A=Fт*h=mgh
A=F*L
mgh = F*L
F = mgh/L =580*10*3/10 =1740 Н =1.74 кН