Пусть скорость , с которой поднимался велосипедист, равна
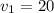
километров в час.
При одинаковом пути в гору и с горы (пусть он равен S) средняя путевая скорость (именно средняя путевая, а не просто средняя) рассчитывается так:

Выразим v2 :

Мы получили значение скорости спуска в общем виде. Подставляем значения скоростей из пп. 1-3:
А)
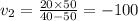
ответ получился отрицательный. Далее напишу, почему так могло произойти
Б)

Здесь тоже ответ не вышел
В)

Почему я упоминал среднюю путевую скорость, а не просто среднюю? Дело в том, что средняя скорость по определению есть отношение модуля перемещения на время перемещения. Здесь велосипедист отправился с одной точки, и в нее же в конечном счёте приехал. Перемещение равно нулю, и средняя скорость тоже.
P.S.S.Почему не получилось ответы? Да все просто: задание некорректно составлено. Если в задаче имелась вдруг в виду средняя арифметическая скорость, то об этом нужно прямо писать.
Средняя арифметическая скорость вычисляется так

Тогда для случаев А, Б, В такие скорости равны соответственно 80, 60 и 40 км/ч
s=s0+v0t+(a/2)t^2 для равноускоренного движения чтобы найти s
v=v0+a*t для равноускоренного движение чтобы найти v
s= v*t для движения с постоянной скоростью
Дано движение с постоянной скорость
v0=3m/s
t0=5s
s0=v0*t0=5*3=15m
Начало движения с ускорением применяем первую формулу
Дано
t0=5s
t2=15
s0=15
v0=3
t=t2-t0
a=20m/s^2
s= s0+v0*t+(a/2)*t^2=15+3*(15-5)+(20/2)*(15-5)^2=15+30+100=145m пройденный путь на конец движения
v=v0+a*t=3+20*(15-10)=203 m/s (это очень быстро настараживает ускорение 20 m/s^2 это очень много вес тела в 2 раза увеличится при таком ускорении по сравнению с обычным состоянием покоя на Земле)
Объяснение:
дано N=1000
S=10^-3 м2
B=1,5 Тл
t=5*10^-4 с
E- ?
по закону Фарадея
модуль ЭДС E1=ΔФ/t=BS/t=1,5*10^-3/5*10^-4=3 В
E=E1*N=3000 В
ответ E=3000 В