Мяч массой 50 грамм ударился о землю с высоты 3 метров и снова взмахнул на высоту 2 метра. На сколько уменьшается его механическая энергия? Как объяснить это законом сохранения энергии?
Во время взрыва на части снаряда действует сила (возможно, непостоянная). Согласно второму закону Ньютона на систему (вообще говоря из нескольких частиц) действует сила:
Здесь мы воспользовались тем, что взрыв происходит очень быстро (я, возможно, рассуждал излишне строго: достаточно показать, что за очень маленькое время импульс меняется незначительно). Тем самым, можем пользоваться сохранением импульса: . Можем умножить скалярно обе части на и воспользоваться тем, что , тогда: , где -- угол между горизонтом и вектором скорости меньшего куска. Импульс в проекции на горизонт: , откуда , потому , с другой стороны, в проекции на вертикаль: , откуда .
Тут, думаю, фишка в том, чтобы считать, что период обращения корабля, летящего по такой орбите, равен периоду обращения корабля, летящего по круговой орбите с радиусом, равны большой полуоси эллипса. Прикинем примерно, что радиус Земной орбиты = 1 а.е., а радиус Марсианской = 1,5 а.е. Ещё из условия нужно догадаться, что такой полёт возможен по единственной траектории, когда занимает ровно половину длины эллипса, то есть положение Земли в момент старта корабля, и положение Марса в момент прибытия , находятся ровно противоположно относительно Солнца. И ещё необходимо привлечь третий закон Кеплера, говорящий о том, что квадраты периодов обращения планет относятся как кубы радиусов их орбит.
Теперь соединим все эти знания в кучку, и попробуем написать уравнение периода обращения корабля вокруг Солнца по такой орбите, как дано в условии.
( Тк / Тз ) ^2 = (Rк / Rз ) ^3 здесь индекс к относится к кораблю, индекс з - к Земле.
Измерять период обращения будем в Земных годах, поэтому считаем Тз = 1. Rк = (Rм + Rз) / 2, здесь индекс м относится к Марсу Подставляем, получаем:
Тк = [ (1,5 + 1 ) / 2 ] ^ (3/2) = 1,4 Земных года, если не ошибся на калькуляторе.
Следовательно, половину орбиты (это и есть время полёта от Земли до Марса по данной траектории, что спрашивается в задаче) корабль пролетит за 1,4 / 2 = 0,7 Земных лет.
Ну, если нигде не накосячил в вычислениях. Лучше проверь за мной.
Во время взрыва на части снаряда действует сила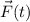 (возможно, непостоянная). Согласно второму закону Ньютона на систему (вообще говоря из нескольких частиц) действует сила:
(возможно, непостоянная). Согласно второму закону Ньютона на систему (вообще говоря из нескольких частиц) действует сила: 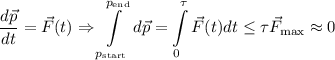
Здесь мы воспользовались тем, что взрыв происходит очень быстро (я, возможно, рассуждал излишне строго: достаточно показать, что за очень маленькое время импульс меняется незначительно). Тем самым, можем пользоваться сохранением импульса: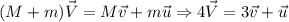 . Можем умножить скалярно обе части на
. Можем умножить скалярно обе части на 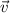 и воспользоваться тем, что
и воспользоваться тем, что 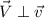 , тогда:
, тогда: 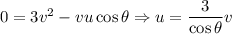 , где
, где 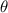 -- угол между горизонтом и вектором скорости меньшего куска. Импульс в проекции на горизонт:
-- угол между горизонтом и вектором скорости меньшего куска. Импульс в проекции на горизонт: 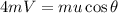 , откуда
, откуда 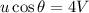 , потому
, потому 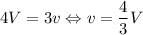 , с другой стороны, в проекции на вертикаль:
, с другой стороны, в проекции на вертикаль:  , откуда
, откуда 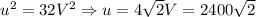 .
.
===
Кажется, немного намудрил