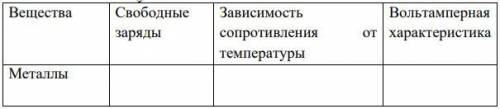

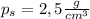
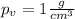

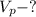
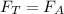 т. к. шар не тонет и не всплывает.
т. к. шар не тонет и не всплывает.
 - объём тела пополам т. к. сила Архимеда действует только на погруженную в воду часть, а по условию шар наполовину погружен в воду.
- объём тела пополам т. к. сила Архимеда действует только на погруженную в воду часть, а по условию шар наполовину погружен в воду.
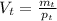
 - обе части уравнения делим на
- обе части уравнения делим на 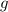 и на
и на 
 - домножаем обе части уравнения на
- домножаем обе части уравнения на 
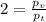 - сделаем уравнение привычнее
- сделаем уравнение привычнее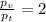 - из уравнения выразим формулу
- из уравнения выразим формулу 
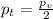
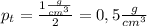
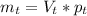
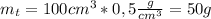
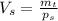
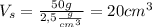
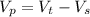

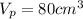 (может отличатся в связи с различной плотностью стекла, я взял плотность оконного)
(может отличатся в связи с различной плотностью стекла, я взял плотность оконного)
на пути h/sin(alpha) на тело действовала сила трения к*m*g*cos(alpha)
на ее преодоление потрачена энергия
h/sin(alpha) * к*m*g*cos(alpha)
остаток энергии будет израсходован на пути х по преодолению силы трения к*m*g
mgh = h/sin(alpha) * к*m*g*cos(alpha) + x*к*m*g
x=h*(1/k -ctg(alpha)) - это ответ
2
тело на высоте h обладало потенциальной энергией mgh и кинетической mv^2/2
на пути h/sin(alpha) на тело действовала сила трения к*m*g*cos(alpha)
на ее преодоление потрачена энергия
h/sin(alpha) * к*m*g*cos(alpha)
остаток энергии будет израсходован на пути L по преодолению силы трения к*m*g
mgh+mv^2/2 = h/sin(alpha) * к*m*g*cos(alpha) + L*к*m*g
v^2 = 2*k*g*h*ctg(alpha) + 2*к*g*L-2*g*h
v = корень(2*k*g*h*(ctg(alpha) + L/р-1/k))