Бедному студенту) имеются 2 цилиндра: алюминиевый (сплошной) и свинцовый (полый) тонкий (m=0,5 кг) одинакового радиуса r=6,0 см и одинаковой массы. за какое время каждый цилиндр скатится без скольжения с наклонной
плоскости? высота наклонной плоскости h=0,50 м, угол наклона плоскости а =30. начальная скорость каждого цилиндра равна нулю.
Будем считать, что сила трения качения пренебрежимо мала, а также пренебрежем сопротивлением воздуха. Тогда для обоих случаев должен выполняться закон сохранения полной механической энергии.
1) Таким образом в обоих случаях цилиндры движутся под действием составляющей силы тяжести параллельной наклонной плоскости. Из второго закона Ньютона получим:
где - ускорение поступательного движения цилиндра.
- ускорение поступательного движения цилиндра.
С другой стороны ускорение равно:
равно:
где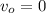 - начальная скорость (по условию)
- начальная скорость (по условию)
Из (1) и (2) найдем искомое время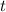 :
:
2) Конечную скорость найдем с закона сохранения механической энергии:
найдем с закона сохранения механической энергии:
где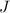 - момент инерции цилиндра относительно его оси симметрии;
- момент инерции цилиндра относительно его оси симметрии;
Подставим в (4) вместо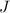 и
и 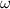 выражения (5) и (6), получим после сокращения:
выражения (5) и (6), получим после сокращения:
Подставим в (3) вместо выражение (7), получим расчетную формулу для искомого времени:
выражение (7), получим расчетную формулу для искомого времени:
Расчет времени:
а) Для сплошного цилиндра, для которого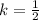 :
:
б) Для тонкостенного цилиндра, для которого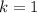 :
: