а)Рассмотрим силы, действующие на человека в лифте. Это сила тяжести mg, сила нормальной реакции опоры N. Проведём ось в ту же сторону, что и ускорение. Запишем второй закон ньютона для этого случая:
mg + N = ma
в проекциях на ось это будет выглядеть как:
N - mg = ma
N = mg + ma = m(g + a)
По 3 закону Ньютона сила реации опры по модулю равна весу:
P = N = m(g+a) = 70(10 + 1) = 70 * 11 = 770 Н
Кстати сказать, в данном случае ускорение направлено вверх, что указывает на то, что лифт разгонялся, а не на то, что он двигался вверх
б)Ускорение направлено вниз. Это означает, что лифт замедлял свою скорость, то ес ть тормозил. На человека в кабине действуют те же силы.
Направим ось y по направлению ускорения, то есть вниз. Запишем второй закон Ньтона в векторной форме:
N + mg = ma
mg - N = ma
N = mg - ma = m(g - a)
P = N - по закону Ньютона.
P = m(g - a) = 70 * 9 = 630 H
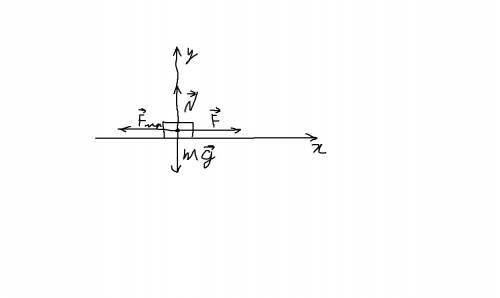
рассмотрим все силы, действующие на брусок.
1)Сила тяги F, направленная по направлению движения бруска.
2)Сила трения F(тр), направленная против движения.
3)Сила тяжести mg, направленная вертикально вниз.
4)Сила реакции опоры, направленная в данном случае вертикально вверх(на самом деле, она всегда направлена перепендикулярно опоре). После решения приложу рисунок, где всё будет показано.
Направим ось x по направлению движения бруска, ось y - вертикально вверх, запишем второй закон Ньютона в векторной форме:
mg + N + F(тр) + F = ma
Мы знаем, что
F(тр) = µN, где µ - коэффициент трения, N - сила реации опоры.
Эту силу найдём из рассмотрения проеций на ось Y закона Ньютона.
N - mg = 0
N = mg
Тогда, F(тр) = µN = µmg = 0.2 * 0.5 * 10 = 1 H
2)В данном случае шкаф не движется потому, что сила трения покоя, возникающая между полом и ножками шкафа, уравновешивается силой, с которой мы действуем на шкаф вдоль поверхности. Сила трения покоя равна по модулю силе, с которой мы действуем на шкаф вдоль поверхности, то есть 50 H.
Дано:
V = 500 л = 500/1000 = 0,5 м³ = 5*10^(-1) м³
p = 0,5 МПа = 5*10^5 Па
v_cр.кв. = 1,5 км/с = 1500 м/с = 15*10^2 м/с
m - ?
pV = (m/M)*RT - уравнение Менделеева-Клапейрона
v_ср.кв. = √((3kT)/m0) - формула средней квадратичной скорости
(v_ср.кв.)² = (3kT)/m0 => T = ((v_ср.кв.)²*m0)/(3k) - выразили температуру из формулы средней квадратичной скорости, тогда:
pV = (m/M)*RT = (m/M)*R*(((v_ср.кв.)²*m0)/(3k)) = m*((v_ср.кв.)²*m0*R)/(M*3k)
Надо преобразовать молярную массу М:
M = m0*Na, где Na - постоянная Авогадро, тогда:
pV = m*((v_ср.кв.)²*m0*R)/(m0*Na*3k) - m0 в числителе и знаменателе сокращается:
pV = m*((v_ср.кв.)²*R)/(Na*3k) - далее можно универсальную газовую постоянную R разложить на составляющие:
R = k*Na, тогда:
pV = m*((v_ср.кв.)²*k*Na)/(Na*3k) - постоянная Больцмана k и постоянная Авогадро Na сокращаются:
pV = m*(v_ср.кв.)²/3 - остаётся выразить массу и найти ей значение:
m = (3*pV)/(v_ср.кв.)² = (3*5*10^5*5*10^(-1))/(15*10^2)² = (15*5*10^4)/(15²*10^4) = 5/15 = 1/3 = 0,(3) = 0,3 кг
ответ: приблизительно 0,3 кг.