
В калориметр, содержащий 1,5 кг воды при 20 C, положили 1 кг льда, имеющего Условие задачи: В калориметр, содержащий 1,5 кг воды при 20 °C, положили 1 кг льда, имеющего температуру -10 °C. Какая температура установится в калориметре? Задача №5.2.37 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ» Дано: m1=1,5 кг, t1=20∘ C, m2=1 кг, t2=−10∘ C, t−? Решение задачи: Из условия задачи совершенно непонятно, растает ли лёд полностью, а может он вообще даже не начнёт плавиться. Значит нам нужно провести оценку. Для начала определим численно количество теплоты Q1, выделяемое водой массой m1 при охлаждении от температуры t1 до температуры плавления льда tп (tп=0∘ C), по формуле: Q1=c1m1(t1–tп) Удельная теплоёмкость воды c1 равна 4200 Дж/(кг·°C). Q1=4200⋅1,5⋅(20–0)=126000Дж=126кДж Далее посчитаем численно количество теплоты Q2, необходимое для нагревания льда массой m2 от температуры t2 до температуры плавления льда tп, по формуле: Q2=c2m2(tп–t2) Удельная теплоёмкость льда c2 равна 2100 Дж/(кг·°C). Q2=2100⋅1⋅(0–(–10))=21000Дж=21кДж И напоследок определим количество теплоты Q3, необходимое для плавления льда массой m2, по следующей известной формуле: Q3=λm2 Удельная теплота плавления льда λ равна 330 кДж/кг. Q3=330⋅103⋅1=330000Дж=330кДж
Источник: https://easyfizika.ru/zadachi/termodinamika/v-kalorimetr-soderzhashhij-1-5-kg-vody-pri-20-c-polozhili-1-kg-lda-imeyushhego/
Для начала вспомним формулу кинетической энергии:
Е=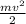
(1) Представим, что мы бросаем этот мяч. Он летит, потом "останавливается" где-то в высшей точке, а потом уже летит вниз. Логично, что если он "останавливается", т.е. не двигается, то и скорость его = 0, следует, по формуле, что кинетическая = 0. ответ 3 верный.
(2) У мяча, пока он летит, скорость не постоянна, иначе как бы он остановился, (так-то еще существуют формулы для свободного падения), значит, что в какой-то момент скорость была наибольшей, а затем начала уменьшаться. Понятно, что скорость максимальна в момент броска. Значит, по формуле кинетическая будет тоже максимальна. ответ 1 неверный.
Неправильность остальных ответов можно объяснить следствиями (2).