Объяснение:
№1
P = IU = I²R
P1/P2 = ( ( 2I )²( R/4 ) )/( I²R ) = ( I²R )/( I²R ) = 1
№2
η = Рпол./Рзат. * 100%
η = ( I2U2 )/( I1U1 ) 100%
I1 = ( I2U2 )/( ηU1 ) 100%
I1 = ( 9 * 22 )/( 90% * 220 ) 100% = 1 A
№3
λ = Тv
λ = 2π√( LCоб. )v
λ = 2π√( L( C1 + C2 ) )v
λ = 2 * 3,14 √( 10 * 10^-3 ( 360 * 10^-12 + 40 * 10^-12 ) ) 3 * 10^8 = 2 * 3,14 √( 10^-2 ( ( 36 + 4 ) 10^-11 ) 3 * 10^8 = 3768 м
№4
WC( max ) = ( CU( max )² )/2
WL( max ) = ( LI( max )² )/2
W = WC( max ) = WL( max )
( CU( max )² )/2 = ( LI( max )² )/2
CU( max )² = LI( max )²
С = ( LI( max )² )/( U( max )² )
W = WC + WL
W = ( CU² )/2 + ( LI² )/2
( CU( max )² )/2 = ( CU² )/2 + ( LI² )/2
CU( max )² = CU² + LI²
LI( max )² = ( LI( max )²U² )/U( max )² + LI²
LI( max )² = L ( I( max )²U² )/U( max )² + I² )
I( max )² = ( I( max )²U² )/U( max )² + I²
Подставим численные данные и решим уравнение
( 5 * 10^-3 )² = ( ( 5 * 10^-3 )²U²/2² ) + ( 3 * 10^-3 )²
2,5 * 10^-5 = 6,25 * 10^-6U² + 9 * 10^-6
( 25 - 9 ) 10^-6 = 6,25 * 10^-6U²
16 = 6,25U²
U = √( 16/6,25 ) = 1,6 B
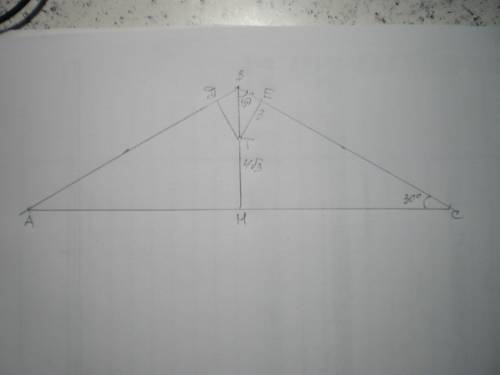
Дано: ΔАВС - равнобедренный, АВ=ВС, ∠В=120°, ДТ=ТЕ=3, ТН=4√3. Найти АС.
∠А=∠С=(180-120):2=30°
Поскольку перпендикуляр - кратчайшее расстояние от точки до прямой, ТЕ⊥ВС, а ΔТВЕ - прямоугольный, где ∠ВЕТ=90°.
Таким же образом точка Т находится на перпендикуляре ВН.
Получаем ВН - высота, медиана и биссектриса ∠В, ∠В=120:2=60°.
Из ΔВТЕ найдем ВТ по теореме синусов:
3\sin60=BT\sin90; BT=3:√3\2=2√3.
ВН=ВТ+ТН=2√3+4√3=6√3.
По теореме синусов найдем СН:
6√3\sin30=CH\sin60
CH=6√3 * √3\2 : 1\2 = 18.
АС=2СН=36 (ед.)
ответ:36 ед.
Потенциальная энергия является скаляром. Чаще всего потенциальную энергию обозначают: Ep,Wp, U.