
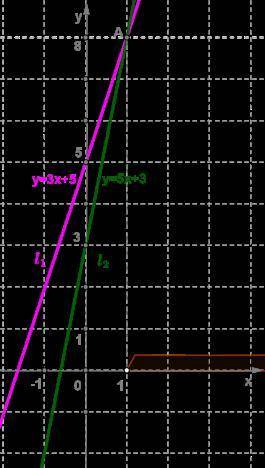
Для решения неравенства 3x+5<5x+3 построим графики линейных функций, расположенных в правой и левой части данного уравнения, т. е. построим графики y=3x+5 и y=5x+3.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции y=3x+5 имеем:
x 0 1
y 5 8
Через полученные точки проведём прямую l1.
Для функции y=5x+3 имеем:
x 0 −1
y 3 −2
Через полученные точки проведём прямую l2.
Прямые y=3x+5 и y=5x+3 пересекаются в точке A(1;8). В этой точке значения функций равны.
Используя построение, делаем вывод: для того чтобы значение первой функции было меньше значения второй функции, необходимо, чтобы первый график был ниже второго, т. е. при x>1.
Можно проверить ответ, полученный при построении, решая неравенство:
3x+5<5x+3;3x−5x<3−5;−2x<−2;x>1.
Объяснение:
ДАНО:
Ho=500 м
V1= 180 км/ч=50 м/с
V2= 24 км/ч=20/3 м/с = 6.67 м/с
п=10 м/с2
L - ?
Решения
скорость падения вымпела имеет ДВЕ составляющих
горизонтальная Vxo=V1= 50 м/с
вертикальная Vyo= 0 м/с
понятно, что вымпел будет падать вертикально до высоты h=0м некоторое время t , найдем время
положительное направление оси ОХ - ВВЕРХ
h=Ho -Vyo*t -gt^2/2 ; h=0м ;Vyo= 0 м/с
gt^2/2 = Ho
t = √ (2Ho/g)
За это же самое время вымпел должен встретится с теплоходом в точке падения
горизонтальная скорость сближения V=V1+V2
тогда расстояние до сброса вымпела
L =V*t= (V1+V2)*√ (2Ho/g)
подставми значения из условия
L = (50+20/3)*√ (2*500/10) = 566.67 м = 0.57 км
проверим единицы измерения
(м/с+м/с) √ (м/м/с2) =м/с √с^2 = м/с *с = м
120 тонн
Объяснение:
1 действие 1000*1440/1,2=1200000 N
2 действие 1200000/10=12000 кг
12000= 12 т