Объяснение:
Дано:
1) x(t) = 3 + 6·t (м)
2) x(t) = 1 + 5·t - t² (м)
______________
S (0) - ?
S (1) - ?
S (1_4) - ?
Первое уравнение:
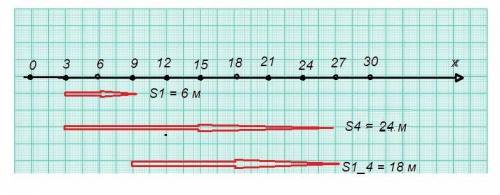
x(t) = 3 + 6·t (м)
Координаты:
x(0) = 3 (м)
x(1) = 3 + 6·1 = 9 (м)
x(4) = 3 + 6·4 = 27 (м)
Модули перемещений:
S(0) = x(0) - x(0) = 3 - 3 = 0 м
S(1) = x(1) - x(0) = 9 - 3 = 6 м
S(4) = x(4) - x(0) = 27 - 3 = 24 м
S(1_4) = x(4) - x(1) = 27 - 9 = 18 м
Второе равнение:
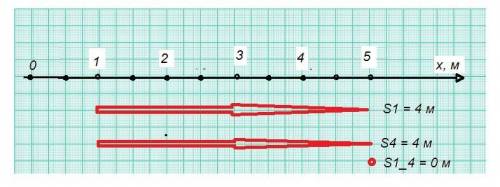
x(t) = 1 + 5·t - t² (м)
Координаты:
x(0) = 1 (м)
x(1) = 1 + 5·1 - 1² = 5 (м)
x(4) = 1 + 5·4 - 4² = 5 (м)
Модули перемещений:
S(0) = x(0) - x(0) = 1 - 1 = 0 м
S(1) = x(1) - x(0) = 5 - 1 = 4 м
S(4) = x(4) - x(0) = 5 - 1 = 4 м
S(1_4) = x(4) - x(1) = 5 - 5 = 0 м
Сделаем чертеж:
1
Объяснение:
в формуле присутствует радиус J=mr^2/2
чем больше радиус тем больше момент инерции.
а теперь на пальцах.
момент инерции - аналогичен массе и имеет смысл как мера инертности для вращательного движения. чем больше момент инерции тем сложнее раскрутить объект и тем сложнее остановить вращающийся объект.
если зафиксировать ось вращения иголки и шестеренки из механического будильника (например в магнитном поле) а потом привести во вращение эти два объекта с одинаковой угловой скоростью, то шестеренка будет вращаться гораздо дольше.
у нее больше момент инерции. она может запасти больше энергии.
большим моментом инерции при равной массе обладают тела, чья масса распределена дальше от оси вращения.
1) T=2*П*корень квадратный из m/k