К космической станции массой М, летящей с выключенными двигателями со скоростью V относительно некоторой инерциальной системы отсчёта вдали от небесных тел, причаливает грузовой корабль массой m. Скорость корабля в той же системе отсчёта равна г и направлена навстречу движению станции. Найдите скорость станции с пристыковавшимся к ней кораблём.
а) для x1 - x0=0 | Для x2 - x0=90
б) проекцию начертишь (см объяснение)
в) В 60м через 1 секунду
Объяснение:
x - координата в момент времени t
x0 - начальная координата
Vx - проекция скорости на ось
Рисуешь линию, отмечаешь 0 и 90, рисуешь стрелки чтобы смотрели друг на друга, где 0 пишешь над стрелкой V1, где 90 соотв. V2, это будет проекция вроде как.
V [м/с]. S=90м (расстояние), V=|V1| + |V2|=90м/с, значит, они встретятся через секунду, записать это можно так: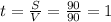
Где встречаются? Если у одного скорость 60м/с, у другого -30м/с, а начальная у первого 0, у второго 90, а время 1с, то 0+60 и 90-30 => 60м
Как-то так. Я в физике на 3-4 учусь, по логике мне проще объяснить, чем по формулам :)