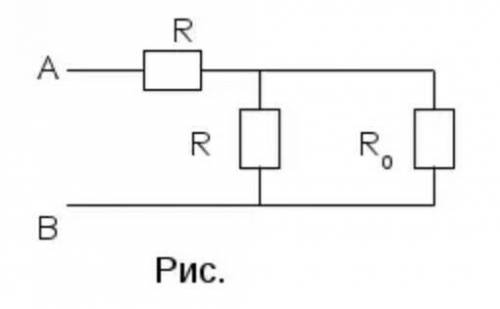
Выделим повторяющийся элемент схемы. В данном случае таким элементом будет такая схема (рис. ) Так как цепочка бесконечна, то при удалении первого элемента сопротивление схемы не изменится. Обозначим общее сопротивление цепочки через RО. Тогда, при удалении первого элемента сопротивление оставшейся цепочки будет также RО, и вместо бесконечной цепочки можно рассматривать такую схему (рис. )
Сопротивление между точками А и В такой схемы:
RAB=R+(R*RO)/(R+RO)
Так как RAB=RO
R=R+(R*RO)/(R+RO)
Решаем полученное уравнение относительно неизвестной величины RО. После приведения к общему знаменателю и группировки подобных членов получим квадратное уравнение
R^2O-RRO-R^2=0
Решая относительно RО, получим
RO=
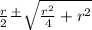
RO=
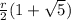
Отрицательный корень отбрасываем, т.к. RО>0.
Подставляя значение R=2 Ом, получаем ответ
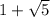
Объяснение:
в начальный момент времени школьники и их камни находятся в точках А и В.
с момента броска камни движутся в поле силы тяжести с одинаковым ускорением направленым вниз
в системе отсчета связанной с нижним камнем верхний движется прямолинейно равномерно (не ускоренно) потому что оба имеют одинаковое ускорение.
относительная скорость второго направлена вдоль вектора BF.
вектор BF состоит из вектора горизонтальной скорости второго камня минус вектор первого.
так как по модулю эти скорости одинаковы то вектор BF направлен под углом 60 градусов к оси х
чтобы найти минимальное расстояние нужно опустить перпендикуляр AD на прямую BD
дальше математика
АВ = BC/sin(30) = h/(0,5) = 2h
AD = AB*sin(30) = 2*h*sin(30)= 2*20*0,5=20 м