Давление жидкости на дно сосуда:
p = ρgh, где ρ - плотность жидкости, кг/м³
g = 9,8 H/кг - ускорение своб. падения
h - высота столба жидкости, м
1). От плотности. Чем больше плотность жидкости, тем большее давление она оказывает при одной и той же высоте столба.
2). От ускорения свободного падения. При удалении от поверхности Земли ускорение свободного падения уменьшается:
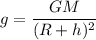
где G = 6,67·10⁻¹¹ H·м²/кг² - гравитационная постоянная
М = 6·10²⁴ кг - масса Земли
R = 6,38·10⁶ м - радиус Земли
h - высота над поверхностью Земли
3). От высоты столба жидкости. Чем больше высота, тем большее давление одна и та же жидкость оказывает на дно сосуда.
Фонарь висит на высоте Н = 286 см.
Объяснение:
Человек, рост которого составляет h = 189 см, стоит под фонарём. Его тень при этом составляет L° = 170 см. Если он отойдёт от фонаря ещё на x = 0,18 м = 18 см, то его тень станет равна L” = 206 см. На какой высоте над землёй висит фонарь?
Чёрный треугольник: Н/h = AD/L° = AD/170; (*)
Красный треугольник: Н/h = AC/L” = AC/206. (**)
Но DС = L”+ x – L° = 206 + 18 – 170 = 54 см. (***)
Делим (**) на (*): 1 = (АС/206)/(AD/170), откуда: (АС/206) = (AD/170) или:
АС = 1,21*AD.
Но из (***): DC = 54 см. Или AC – AD = 54. ==> 1,21*AD – AD = 54 ==> 0,21*AD = 54 ==> AD = 257,1 см.
Подставив AD в (*), получим: 170*H = h*AD ==> H = h*257,1/170 = 189*257,1/170 = 285.8 см.
Итак, фонарь висит на высоте Н = 286 см.
Из закона Георга Ома для полной цепи следует:
I=E/(R+r) =>
Rᴀ=E/I-r=36/8-3=1,5 Ом.