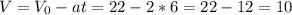 м/с
м/с
1) для того, чтобы найти момент времени, в который скорости обеих точек будут одинаковыми, приравняем формулы конечных скоростей обеих точек
для первой точки имеем V1 = V01 + a1 t
для второй V2 = V02 + a2 t
получаем
V01 + a1 t = V02 + a2 t
t (a1 - a2) = V02 - V01
t = (V02 - V01) / (a1 - a2)
t = (6 - 3) / (-0,2 + 0,8) = 3 / 0,6 = 5 c
пояснение: V01 и V02 - это начальные скорости точек, которые можно определить по уравнению координаты (x = x0 + V0x t + a(x) t^2 / 2). тоже самое и с ускорениями
2) собственно, про ускорения: они даны по условию. можно заметить из написанного выше уравнения координаты, что ускорение делится пополам. значит, для первой точки ускорение равняется a1 = - 0,2 м/с^2, а для второй точки a2 = - 0,8 м/с^2
3) для определения скоростей точек, воспользуемся формулой V = V0 + a t
имеем для первой точки V1 = V01 + a1 t
V1 = 3 - 0,2 * 5 = 2 м/с
соответственно для второй точки V2 = V02 + a2 t
V2 = 6 - 0,8 * 5 = 2 м/с
Амплитуда - это отклонение маятника от положения равновесия. На графике амплитудой являются максимумы и минимумы косинусоиды. Это будут 2 и -2. Когда говорят просто определить амплитуду, то имеется в виду модуль амплитуды:
|A| = |2| = |-2| = 2 м
Период - это время, за которое маятник делает одно колебание. На графике периоду соответствует цифра 5, потому что участок косинусоиды до цифры 5 изменяется без повторов, а в момент времени 5 с начинается новое колебание (начинается повтор). Частота колебаний - это величина обратная периоду. То есть:
Т = 5 с
v = 1/T = 1/5 = 0,2 Гц