
Состояние определенной массы любого вещества можно описать с трех параметров: давления
p
, объема
V
и температуры
T
. Эти параметры связаны между собой. Их взаимосвязь описывается уравнением состояния, которое в общем случае имеет вид:
F
(
p
,
V
,
T
)
=
0.
Конкретный вид уравнения зависит от свойств вещества. Например, разреженный газ при достаточно высокой температуре хорошо описывается моделью идеального газа. Уравнением состояния для него является известное уравнение Клапейрона (
1799
−
1864
), предложенное в
1834
году:
p
V
=
m
M
R
T
.
Здесь
m
− масса газа,
M
− молярная масса (т.е. масса одного моля данного газа),
R
− универсальная газовая постоянная. Для одного моля газа это уравнение принимает следующий вид:
p
V
=
R
T
.
Проведенные позднее эксперименты выявили отклонение в поведении реальных газов от законов идеального газа. Эти результаты были обобщены голландским физиком Яном Дидериком Ван-дер-Ваальсом (
1837
−
1923
), который в
1873
году предложил более точное уравнение состояния реального газа. Оно называется уравнением Ван-дер-Ваальса и в расчете на один моль записывается в виде
(
p
+
a
V
2
)
(
V
−
b
)
=
R
T
.
Данное уравнение учитывает силы притяжения и отталкивания, действующие между молекулами. Силы притяжения учитываются благодаря пристеночному эффекту. Действительно, для частиц, находящихся во внутренней области, силы притяжения со стороны других молекул в среднем скомпенсированы. Однако для частиц вблизи стенок сосуда возникает нескомпенсированная сила притяжения
f
,
направленная внутрь сосуда. Эта сила, с одной стороны, пропорциональна концентрации частиц
n
в сосуде, а с другой стороны − пропорциональна концентрации частиц в пристеночном слое. В результате получаем:
f
∼
n
2
∼
1
V
2
,
где
n
− концентрация молекул в сосуде,
V
− объем
1
моля газа.
Рассмотренный эффект притяжения молекул пристеночного слоя приводит к уменьшению давления на стенки сосуда. При формальном переходе от уравнения Клапейрона к уравнению Ван-дер-Ваальса это соответствует замене
p
→
p
+
a
V
2
,
где
a
− коэффициент, зависящий от конкретного газа и размеров сосуда.
Силы отталкивания между молекулами в модели Ван-дер-Ваальса учитываются очень просто: предполагается, что молекулы имеют форму шара радиуса
r
и не могут приблизиться друг к другу на расстояние между центрами, меньшее чем
2
r
.
Можно считать, что вокруг одной из двух молекул существует "запрещенный" (исключенный) объем (рисунок
1
), равный
4
3
π
(
2
r
)
3
=
8
⋅
4
3
π
r
3
.
Следовательно, в расчете на одну молекулу исключенный объем равен
b
0
=
4
⋅
4
3
π
r
3
=
4
V
0
,
где
V
0
− объем одной молекулы.
В результате , если в уравнении Клапейрона объем пространства, доступного для движения молекул, был равен
V
,
то теперь он становится равным
V
−
N
A
b
0
=
V
−
b
,
где
N
A
− число Авогадро (равное числу молекул в одном моле газа),
b
− исключенный объем, обусловленный отталкиванием молекул.
Объяснение:
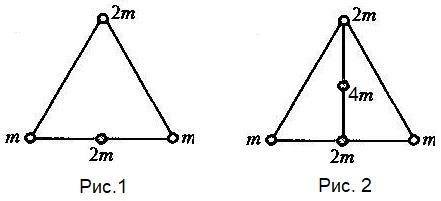
Рассмотрим два нижних шарика. Так как их массы одинаковы, их центр тяжести 2m лежит на середине нижней стороны треугольника, соединяющей эти шарики (Рисунок 1). Задача сводится к определению центра тяжести системы двух шариков - верхнего, массой 2m и нижнего с такой же массой 2m. Очевидно, что центр тяжести системы этих двух шариков 4m, а значит и всей системы в целом, лежит на середине стороны, соединяющей эти два шарика. Так как треугольник равносторонний, то медиана, проведенная к нижней стороне треугольника является и биссектрисой верхнего угла. Значит искомый центр тяжести лежит на середине биссектрисы верхнего угла, в котором находится шарик массой 2m (Рисунок 2).
ответ: Центр тяжести системы шариков находится на середине биссектрисы угла, в котором находится шарик массой 2m.
ответ: Второй ответ: Остановить движение катушки.
Объяснение:
Проверено Билимлендом)