Дано:
α=30°;
t₁=2 c;
t₂=4 c;
_______
Найти: L
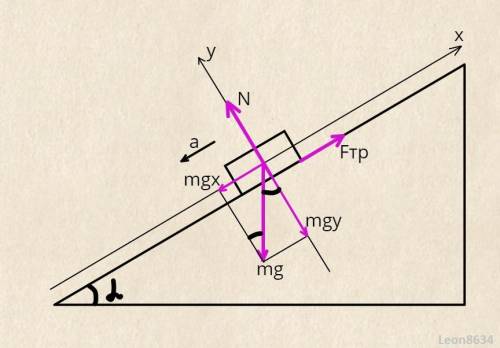
Изобразим все силы, действующие на камень (см. рисунок). При этом учтем влияние силы трения, так как нигде не указано что плоскость гладкая.
Запишем второй закон Ньютона для движения вверх и вниз:
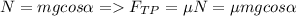 - на ось Оу для обоих случаев одинаков
- на ось Оу для обоих случаев одинаков
 - на ось Ох для движения вверх
- на ось Ох для движения вверх
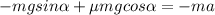 - на ось Ох для движения вниз.
- на ось Ох для движения вниз.
Выразим отсюда ускорения камня:
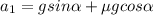 - вверх
- вверх
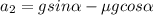 - вниз
- вниз
Важно помнить, что оба ускорения направлены вдоль наклонной плоскости вниз. Запишем уравнения кинематики камня:
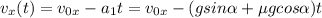 - скорость вверх
- скорость вверх
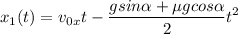 - координата вверх
- координата вверх
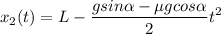 - координата вниз
- координата вниз
С учетом условий задачи:
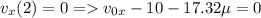 - условие остановки в верхней точке
- условие остановки в верхней точке
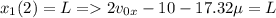 - прохождение пути L вверх
- прохождение пути L вверх
 - прохождение пути L вниз
- прохождение пути L вниз
Выразим L из последнего, а начальную скорость из первого уравнения и подставим во второе:

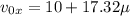
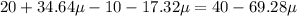
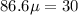
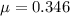
Искомая длина:
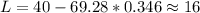 м
м
ответ: 16 м.
с постоянной скоростью v0 самолет затратит на перелет между городами, расстояние между которыми S, время t1 = (2S)/v0 = 6 ч
следовательно, расстояние между городами S = (v0 t1)/2
• с ветром
при наличии ветра, скорость самолета v будет геометрически складываться из его собственной скорости v0 и скорости ветра u. используя теорему Пифагора, находим
v = √(v0² - u²)
значит, в этот раз время перелета равно
t2 = 2S/√(v0² - u²) = 6.15 ч
учитывая, что S = (v0 t1)/2, получаем
t2 = (v0 t1)/√(v0² - u²)
v0 t1 = t2 √(v0² - u²)
v0² t1² = t2² (v0² - u²)
u = (v0 √(t2² - t1²))/t2
u = (91.2*sqrt(6.15^(2)-36))/6.15 ≈ 20.02 м/c