ответ:1. Многоуровневый рычаг в целом состоит из трёх рычагов. Для того чтобы вся система находилась в состоянии равновесия, в равновесии должен находиться каждый отдельный рычаг.
На рисунке внизу видно, что всего имеется шесть плечей силы. Значения их длин необходимо определить по рисунку, приведённому в задании:
l1=2,l2=1,l3=1,l4=3,L1=4,L2=2.
2. Прежде всего имеется возможность определить массу противовеса m2, при которой верхний левый рычаг будет находиться в равновесии. Для этого необходимо использовать условие равновесия рычага: F1⋅l1=F2⋅l2.
Так как сила тяжести, создаваемая противовесом, пропорциональна его массе, то вместо силы тяжести можно использовать массу, получив таким образом:
m2=m1⋅l1l2=32⋅21=64кг.
3. Для того чтобы нижний рычаг находился в состоянии равновесия, необходимо выполнение условия: (m1+m2)⋅L1=(m3+m4)⋅L2, что позволяет узнать общую массу 3-го и 4-го противовеса:
(m3+m4)=(m1+m2)⋅L1L2=(32+64)⋅42=192кг.
4. Чтобы верхний правый рычаг находился в состоянии равновесия, общая масса m3+m4 должна распределяться обратно пропорционально плечам силы рычага, то есть:
m3m4=l4l3=31.
Таким образом получаем систему уравнений:
{m3+m4=192m3=31⋅m4
Подставляя в первое уравнение выражение для m3, из второго уравнения получаем:
31⋅m4+m4=(3+1)⋅m4=192.
После выполнения преобразований получаем:
m4=192(3+1)=48кг.
5. m3 определяют из выражения для общей массы правого верхнего рычага m3=192−m4=192−48=144кг.
Рычаг находится в равновесии, если массы противовесов равны:
m2=64кг,
m3=144кг,
m4=48кг.
Объяснение:
Частота - это число колебаний в единицу времени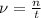 , где n - число колебаний, t - промежуток времени (с). Вычислим:
, где n - число колебаний, t - промежуток времени (с). Вычислим: 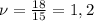 Герц.
Герц.
Период обратен частоте т.е.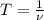 . Вычислим:
. Вычислим: 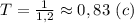
По формуле математического маятника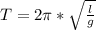 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). В системе СИ: 40 см = 0,4 метра. Подставляем числовые значения и вычисляем: 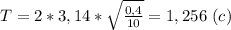
По формуле математического маятника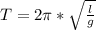 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период:
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²). Подставляем и вычисляем: период: 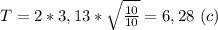
Частота следовательно будет равна: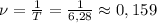 Гц
Гц
Используем две формулы периода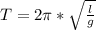 , где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и
, где l - длина маятника (м), g - ускорение свободного падения (g = 9,8 м/с² ≈ 10 м/с²) и 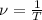
Левые части формул равны, следователь и правые части также равны:
Распишем частоту: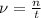
Подставляем и вычисляем: