ОЧЕНЬ НУЖНА ! Источники света излучают свет с частотой 10^14 Гц. Расстояние между источниками равно 6 м. Что будет наблюдаться в результате интерференции в точке лежащей на прямой, соединяющей источники, на расстоянии 3 м 30 см от первого источника?
Пусть площадь льдины S, плотности льда и воды кг/м3 и кг/м3 соответственно, толщина льдины м, масса человека кг, ускорение свободного падения .
Человек будет держаться на воде, если сила тяжести человека и льдины будет компенсироваться силой Архимеда, наименьшая подходящая площадь получится, если льдина полностью скроется под водой.
Объём льда Масса льда Суммарная масса льдины и человека Сила тяжести Сила Архимеда
Приравниваем силу тяжести и силу Архимеда и находим S:
тело начинает соскальзывать с вершины полусферы начальная скорость соскальзывания v0 определяется из закона сохранения импульса в момент попадания пули mV=(M+m)*v0, откуда v0=m*V/(M+m) Скорость на высоте h от земли определяется из закона сохранения энергии (M+m)v0^2/2+(M+m)gR=(M+m)v^2/2+(M+m)gh Откуда v^2=v0^2+2g(R-h) Надо записать силы, дейст(M+m)вующие на тело (с пулей внутри), когда оно находится на высоте h от земли (ещё не соскользнув с полусферы). Тут нужен рисунок Сила тяжести (M+m)g вниз Сила реакции опоры N в точке контакта тела и полусферы в направлении к телу Равнодействующая этих сил имеет проекцию как на направление к центру полусферы, так и на направление касательной к полусфере в точке контакта. Первая проекция соответствует центростремительному ускорению, вторая тангенциальному ускорению, то есть изменению скорости тела. Для нас важна только первая проекция. Проектируем силу тяжести на направление нормали (Угол между вертикалью и направлением нормали обозначаем альфа, тогда cos альфа =h/R), получаем (M+m)g cos альфа=(M+m)gh/R Тогда проекция равнодействующей на направление нормали (M+m)gh/R-N По второму закону Ньютона эта проекция должна быть равна (M+m)a_n, где a_n (a с индексом n) -- центростремительное ускорение v^2/R=(v0^2+2g(R-h))/R (M+m)gh/R-N=(M+m)(v0^2+2g(R-h))/R, откуда находим, что N=(M+m)gh/R-(M+m)(v0^2+2g(R-h))/R По мере соскальзывания тела со сферы, сила реакции будет уменьшаться, в момент отрыва тела от сферы она будет равна нулю, приравнивая её нулю и найдём h (M+m)gh/R-(M+m)(v0^2+2g(R-h))/R=0 умножим на R разделим на (M+m) gh-(v0^2+2g(R-h))=0 gh-v0^2-2gR+2gh=0 3gh=2gR+v0^2 h=(2gR+v0^2)/3g, осталось подставить v0 и дело в шляпе
2,3 м²
Объяснение:
Поверхностное натяжение не учитываем.
Пусть площадь льдины S, плотности льда и воды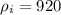
кг/м3 и 
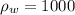кг/м3 соответственно, толщина льдины 
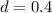м, масса человека 
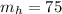кг, ускорение свободного падения 
.
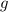Человек будет держаться на воде, если сила тяжести человека и льдины будет компенсироваться силой Архимеда, наименьшая подходящая площадь получится, если льдина полностью скроется под водой.
Объём льдаПриравниваем силу тяжести и силу Архимеда и находим S:
S = 75 кг / (80 кг/м3 * 0,4 м) = 2,3 м2