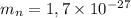кг, радиус 
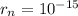м. Полагая, что в нейтронной звезде нейтроны плотно упакованы, оцените радиус нейтронной звезды, если её масса равна солнечной. 2. При термоядерных реакциях во время образования одного ядра гелия выделяется энергия 
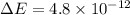Дж Светимость Солнца 
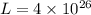Вт. Определите, сколько гелия образуется на Солнце каждую секунду.
Объяснение:
Дано:
m(в-ва)= 450 г= 0,45 кг
m(в)= 200 г= 0,2 кг
t1=23°С ; t2= 30°С; T = 100°С
C-?
По условию теплоемкостью калориметра можно пренебречь, тогда после установления теплового равновесия при изменении температур вода получила определенное количество тепла, а вещество потеряло это же количество тепла. Отсюда имеем уравнение теплового баланса
Сm(в)(t2-t1)=Cm(в-ва)(T-t2) где С= 4200Дж/кг*С удельная теплоемкость воды.
Удельная теплоемкость равна:
С(в-ва)=Сm(в)(t2-t1)/m(в-ва)(T-t2) = 4200*0,2(30-23)/0,45(100-30)= 5880/31,5 ≈ 187Дж/кг*С
Мне так представляется, что ускорение мела (замедление, если угодно, отрицательное ускорение) в данной задаче постоянно.
Почему так?
Сила трения Fтр = N * mu = m * g * mu
Ускорение (как учил старина Ньютон) а = F / m.
В направлении движения, на мел действует единственная сила - трения, других я из условия не усматриваю.
Следовательно, ускорение
а = m * g * mu / m = g * mu = 10 * 0,3 = 3 м/с2
Обычное тело в таких условиях ехало бы путь
Х = v^2 / (2a) = 121 / 6 = 20,1666 м, но эх, какая незадача - мел истирается. Ок, так сколько же метров сможет вообще проехать мел до полной аннигиляции при условии заданных цифр?
х = 8 г / 0,5 г/м = 16 м. Жаль, недолог его путь. Но зато мы уже более близки к ответу.
Чисто технически мне проще сначала найти скорость u мела в момент его исчезновения.
х = ( v^2 - u^2 ) / (2a)
16 = (121 - u^2) / 6
u^2 = 25
u = 5 м/с - при этой скорости от мела, как от чеширского кота, остаётся лишь наглая глумливая ухмылка, и больше ничего.
Отсюда поищем время от начала движения до сего печального момента:
t = (v-u) / a = (11-5) / 3 = 2 c
Ну, может я ошибаюсь, но мне так кажется. Если, конечно, мел не украдут раньше в пути его следования.