Задача на бросок под углом к горизонту. Уравнения движения камня:
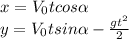
По условию, траектория камня проходит через точку с координатами  = 20 и
= 20 и 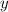 = 15.
= 15.
Имеем систему:
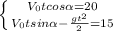
Из первого уравнения выразим время 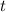 и подставим во второе уравнение:
и подставим во второе уравнение:
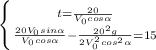
Преобразуем второе уравнение:
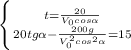
Из второго уравнения несложно выразить 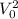 :
:
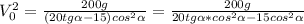 (&)
(&)
Для того, чтобы 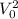 было наименьшим, необходимо, чтобы знаменатель дроби в правой части принимал как можно большее значение, так как величина числителя фиксирована.
было наименьшим, необходимо, чтобы знаменатель дроби в правой части принимал как можно большее значение, так как величина числителя фиксирована.
Заметим, что 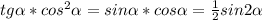 , а также
, а также 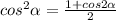 (формулы двойного угла).
(формулы двойного угла).
Тогда
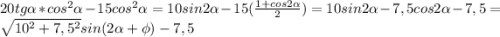
(в последнем переходе воспользовались формулой вс аргумента).
Понятно, что максимальное значение 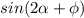 это 1. Тогда максимальное значение выражения
это 1. Тогда максимальное значение выражения 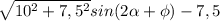 есть
есть 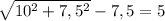 .
.
Возвращаясь к выражению (&), имеем:
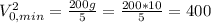 , отсюда
, отсюда 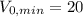 м/с.
м/с.
Обозначения:
V - объём
m - масса
p - давление
Wк - средняя кинетическая энергия
n - концентрация молекул
Nₐ - постоянное число Авогадро
M - молярная масса молекул
m₀ - масса одной молекулы
υ - средняя квадратичная скорость
N - число молекул
Дано: V = 2 м³; m = 2,5 кг; p = 1,5 × 10⁵ Па; Nₐ ≈ 6,02 × 10²³ моль⁻¹.
Найти: Wк - ?
Решение. Средняя кинетическая энергия определяется из основного уравнения молекулярно-кинетической теории (уравнения Клаузиуса), которая связывает микропараметры и макропараметры: p = m₀nυ²/3, где Wк = m₀υ²/2 ⇒ р = 2nWк/3 ⇒ Wк = 3р/2n. Концентрация молекул (n) находится по формуле n = N/V, где N = mNₐ/M ⇒ n = mNₐ/VM, где M(N) = Ar(N) = 14 г/моль = 14 × 10⁻³ кг/моль.
Значит, Wк = 3р/2n = 3рVM/2mNₐ.
Определим значение искомой величины:
[Wк] = (Па×м³×кг/моль)/кг×моль⁻¹ = Н×м³×кг×моль/моль×кг×м² = Н×м = Дж
Wк = 3×1,5 × 10⁵×2×14 × 10⁻³/2×2,5×6,02 × 10²³ = 126×10²/30,1×10²³ ≈ 4,2 × 10⁻²¹ Дж = 4,2 зДж
ответ: 4,2.