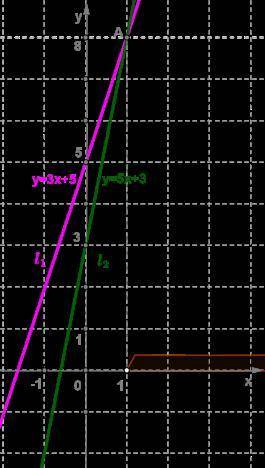
Для решения неравенства 3x+5<5x+3 построим графики линейных функций, расположенных в правой и левой части данного уравнения, т. е. построим графики y=3x+5 и y=5x+3.
Для построения графика каждой линейной функции составим таблицу значений.
Для функции y=3x+5 имеем:
x 0 1
y 5 8
Через полученные точки проведём прямую l1.
Для функции y=5x+3 имеем:
x 0 −1
y 3 −2
Через полученные точки проведём прямую l2.
Прямые y=3x+5 и y=5x+3 пересекаются в точке A(1;8). В этой точке значения функций равны.
Используя построение, делаем вывод: для того чтобы значение первой функции было меньше значения второй функции, необходимо, чтобы первый график был ниже второго, т. е. при x>1.
Можно проверить ответ, полученный при построении, решая неравенство:
3x+5<5x+3;3x−5x<3−5;−2x<−2;x>1.
Объяснение:
вот
Объяснение:
Stress
Интенсивность внутренних сил в определенной точке данного сечения.
79. Нормальное напряжение
Normal stress
Составляющая напряжений, направленных по нормали к площадке ее действия.
80. Касательное напряжение
Shearing stress
Составляющая напряжений, лежащих в плоскости сечения.
81. Переменное напряжение
Alternate stress
Напряжения, переменные во времени, возникающие в элементах конструкции под действием нагрузок, переменных по величине или направлению, а также нагрузок, перемещающихся относительно рассматриваемого элемента.
82. Допускаемое напряжение
Allowable stress
Экспериментально установленное для рассматриваемого материала предельное значение напряжения, деленное на коэффициент запаса прочности.
83. Главное напряжение
Principal stress
Среди множества площадок, которые можно провести через исследуемую точку, имеются три взаимно перпендикулярные площадки, касательные напряжения на которых отсутствуют. Эти площадки и возникающие на них нормальные напряжения называются главными.
84. Эквивалентное (приведенное) напряжение
Equivalent stress
Напряжение одноосного растяжения (сжатия), равноопасного рассматриваемому сложному напряженному состоянию.