Гов но — разговорное название продуктов жизнедеятельности живых существ
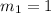 кг
кг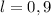 м
м °
° кг
кг м/с
м/с м/с
м/с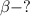
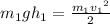
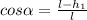
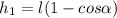
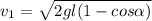
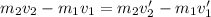 ,
,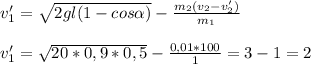

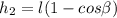
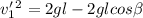
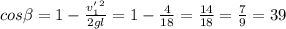 °
°
несобственные, кратные.
Решение интегралов онлайн »
Несобственный интеграл »
График функции
Это сервис построения графиков на плоскости и в пространстве. Приводится подробное решение на исследование функции.
Построение графиков функций »
График неявной функции »
Построение поверхности »
Решение систем неравенств
Вы можете попробовать решить любую систему неравенств с данного калькулятора систем неравенств.
Решение системы неравенств »
Комплексные числа
Здесь можно вычислить комплексные выражения: находить формы (алгебраическую, тригонометрическую, показательную); модуль и аргумент, сопряжённое, геометрическую интерпретацию.
Комплексные числа »
Решение матриц
Такие действия как умножение, обратная матрица, транспонирование матриц, сумму, ранг матрицы, возведение матриц в степень, нахождение определителя матрицы можно провести здесь.
Вы получите подробное решение. Для этого необходимо выполнить простые шаги - ввод матрицы или ввод числа в зависимости от действия.
Решение матриц »
Какая биогия где вапросы где ответы ептп